Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
$2+2=2\cdot2$
Tenhle triviální vztah nikoho nepřekvapí. Pro která další dvě přirozená (kladná) čísla platí, že jejich součet se rovná jejich součinu?Řešení
Ostrov pohanů
Velký mořeplavec Tomáš Kuchař kdysi objevil ostrov, na kterém v 27 vesnicích na pobřeží žijí pohané. Vesnice objel podle pobřeží jednu za druhou a označil je na mapě postupně 27 písmeny abecedy A, B, ..., Z (písmena s háčky mohl vynechat). Řád bosonohých Ferdinandů zahrnoval 27 bratří, jméno každého z nichž začínalo právě jedním z 27 písmen abecedy. Považovali to za Boží znamení, že mají právě oni obrátit pohany v těch 27 vesnicích na pravou víru. Vylosovali jednoho z bratrů, poslali ho na ostrov, a protože se domnívali, že systematický postup nejlépe povede ke kýženému výsledku, vyslaný misionář se měl vylodit ve vesnici, jejíž jméno začíná stejným písmenem jako jeho jméno, a přivést zdejší pohany k víře. Jakmile to udělá, měl se přesunout do následující vesnice ve směru proti pohybu hodinových ručiček a obrátit její obyvatele na víru. Atd. Když o misionáři po delší dobu neměli zprávu, vylosovali dalšího a poslali ho se stejným úkolem na ostrov. Netušili, že problém byl v tom, že pohanští obyvatelé vesnice se docela ochotně nechali obrátit na víru, ale jakmile do takové již obrácené vesnice přišel misionář (ten, který tam už byl nebo jiný), usoudili, že toho je příliš, misionáře snědli a vrátili se k pohanství. Protože v řádu neměli od vyslaných misionářů žádné zprávy, mohlo se stát, že jich na ostrově současně působilo několik najednou, aniž o sobě věděli. Kolik vesnic na ostrově bude obráceno na víru, až ostrov navštíví poslední z 27 bratrů a dokončí svou misi?Řešení
Rovnoběžník a rovnostranné trojúhelníky
Na obrázku je rovnoběžník $ABCD$, k jehož stranám $AB$, $AD$ přiléhají rovnostranné trojúhelníky $AEB$, $ADF$.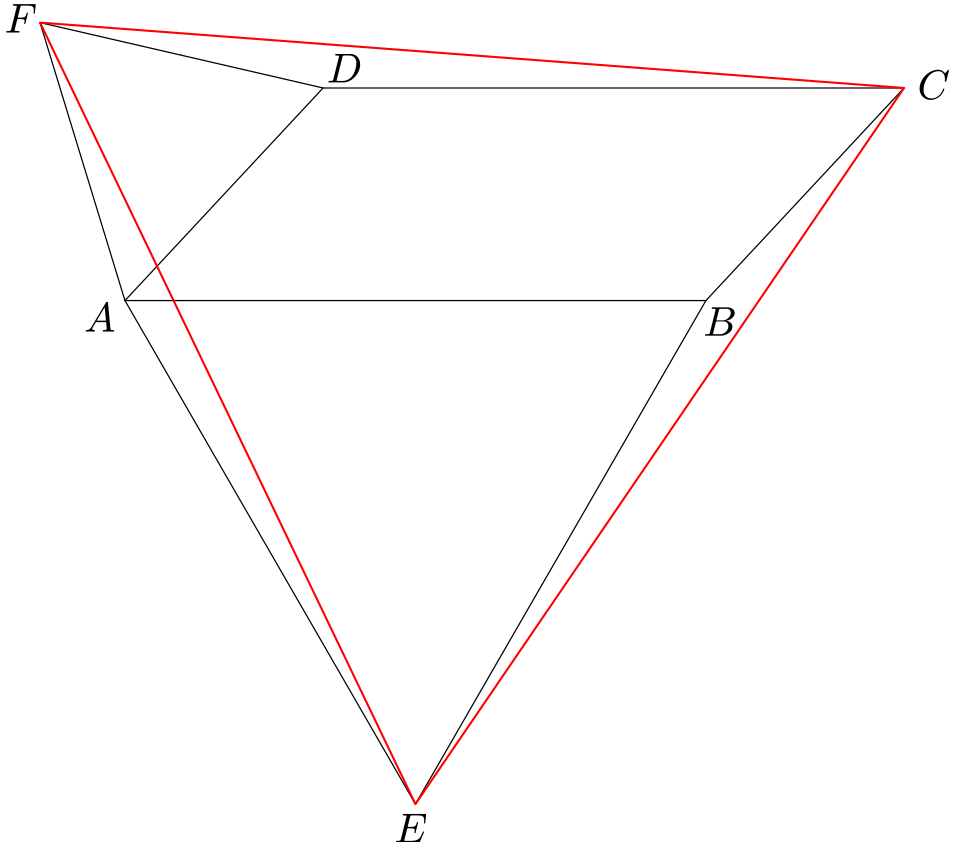
Řešení
Archiv úloh z předchozích týdnů
Příbuzenské vztahy
Příbuzenský vztah je vzájemný (v matematickém jazyce symetrický, tj. A je příbuzný B, právě když je B příbuzný A). Umíte dokázat, že na každé společenské akci jsou alespoň dva lidé se stejným počtem příbuzných?
Řešení
Chuck a Luck
Chuck a Luck je jednoduchá hazardní hra se třemi kostkami pro libovolný počet hráčů, která má původ ve staré Číně. Každý hráč si vsadí na některé z čísel $1, 2,\dots, 6$. Bankéř hodí třemi kostkami. Jestliže ani na jedné kostce nepadne vybrané číslo, hráči jeho sázka propadá. Jestliže vybrané číslo padne, hráč si vezme zpět svou sázku a bankéř mu přidá odměnu podle předem dohodnutého klíče. Uvažujme variantu klíče 1-2-3, tj. padne-li zvolené číslo na jediné kostce, bankéř vyplatí odměnu rovnou vsazené částce, padne-li zvolené číslo na dvou kostkách, vyplatí dvojnásobek, a padne-li zvolené číslo na všech kostkách, vyplatí trojnásobek vsazené částky. Jaké má hráč vyhlídky v takové hře? Je klíč 1-2-10 lepší nebo horší? A co 1-3-5?
Řešení
Úhly mezi tětivou, osou úhlu a výškou
V trojúhelníku $ABC$ s pravým úhlem při vrcholu $C$ svírají výška $CK$, osa $CL$ úhlu při vrcholu $C$ a tětiva $CM$ úhly $\alpha$ a $\beta$.
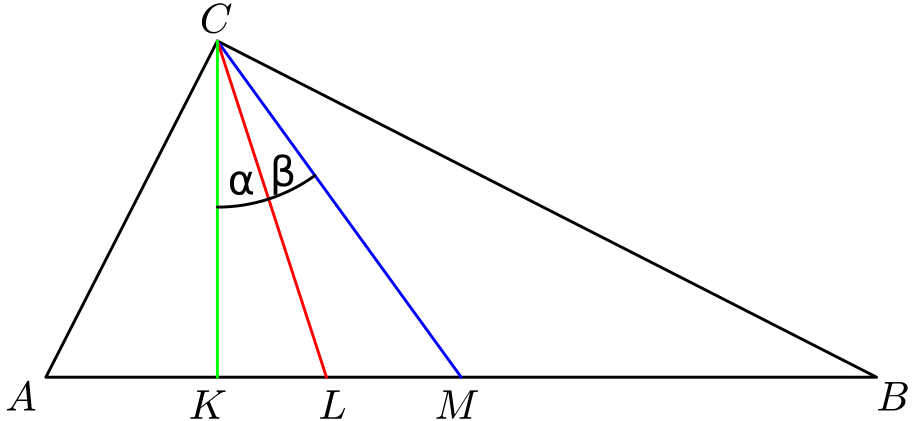
Řešení
Cesta z nádraží
Paní Nováková dojíždí vlakem do práce. Při cestě domů přijíždí pravidelně v 17:00 hodin. Pan Novák, který je již v důchodu, pro ni jezdí autem na nádraží a přijíždí tam přesně v 17:00. Jednou se stalo, že paní Nováková přijela vlakem o hodinu dřív. Panu Novákovi se nedovolala, bylo pěkné počasí, a tak vyrazila k domovu pěšky. Po cestě potkala pana Nováka, který jel jako obvykle pro ni nádraží, přisedla k němu do auta a domů dorazili o 20 minut dřív než obvykle. Při jiné takové příležitosti se situace opakovala s tím rozdílem, že na nádraží přijela v 16:30. O kolik minut dříve než obvykle dorazili domů tentokrát za předpokladu, že pan Novák jezdí na nádraží a zpět pokaždé stejnou cestou a stejnou rychlostí a paní Nováková chodí také pokaždé stejnou rychlostí?Řešení
Barevné vrcholy obdélníků
Rozdělme všechny body v rovině do dvou množin, tak že každý z nich patří právě do jedné z nich. Dokažte, že v rovině existuje obdélník, jehož všechny čtyři vrcholy patří do jedné z těchto množin.Řešení
Zajímavé vztahy v trojúhelníku
V ostroúhlém trojúhelníku $ABC$ je přímka $AE$ osou úhlu při vrcholu $A$ a přímka $BD$ je osou úhlu při vrcholu $B$. Bod $P$ je patou kolmice spuštěné z bodu $C$ na přímku $BD$ a bod $Q$ je patou kolmice spuštěné z bodu $C$ na přímku $AE$.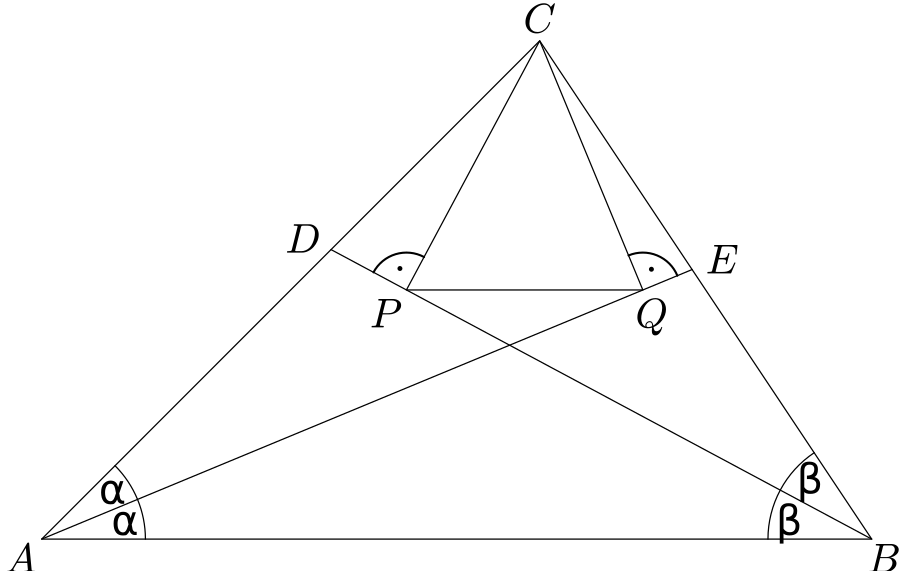
Řešení
Hra s čísly
Jednoduchá hra s čísly pro dva hráče probíhá následovně. Hráči na papír napíšou řadu přirozených čísel od 1 do $n$, kde $n$ je liché číslo. Hráči střídavě škrtají jednotlivá čísla, až zůstanou poslední dvě nepřeškrtnutá. Začínající hráč zvítězí, pokud jsou zbývající dvě čísla nesoudělná, jinak vítězí soupeř. Co si vyberete? Začínat, nebo hrát jako druhý?Řešení
Zajímavá vlastnost složených čísel
Přirozená čísla, která nejsou prvočísly, se nazývají složená. Složené číslo lze tedy alespoň dvěma různými způsoby rozložit na součin dvou přirozených čísel, např. $6=1\cdot6=2\cdot3$. Sečteme-li druhé mocniny čtyř čísel v obou rozkladech, dostaneme $1^2+6^2+2^2+3^2=50$. Výsledné číslo $50$ je opět složené. Dokažte, že to platí vždy, tj. je-li složené číslo $n$ vyjádřeno jako $n=ab=cd$, kde $a\ne c$ a $a\ne d$, pak číslo $a^2+b^2+c^2+d^2$ je vždy složené, nikdy to není prvočíslo.Řešení
Menelaova věta
Menelaos z Alexandrie (asi 70–140 n. l.) byl řecký matematik a astronom. Byl prvním, kdo definoval sférický trojúhelník (geometrický útvar na povrchu koule určený třemi hlavními kružnicemi; na kulovém glóbu ho např. tvoří dva poledníky a rovník). Připisuje se mu následující věta. V rovině je dán trojúhelník $ABC$ a tři body $P$, $Q$, $R$ ležící na přímkách $BC$, $AC$ a $AB$. Jestliže tyto body leží na téže přímce, pak platí ${AR\over RB}\cdot{BP\over PC}\cdot{CQ\over QA}=-1$, kde $XY\over YZ$ označuje podíl délek úseček $XY$ a $YZ$ se znaménkem plus, je-li bod $Y$ mezi body $X$, $Z$, a v opačném případě se znaménkem minus. Mohou nastat dva případy podle toho, jestli přímka $PR$ protíná trojúhelník $ABC$
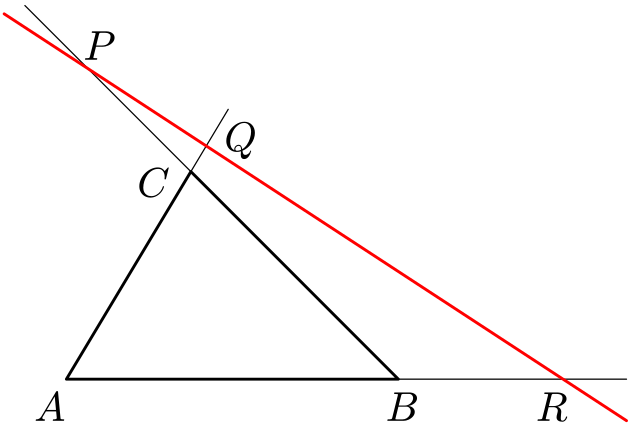
Řešení
Příliš složitý výpočet?
Některé úlohy z praxe převedené do matematického jazyka vedou na poslouponosti $\{a_n\}$, $n=1,2,\dots$, definované rekurentně tak, že je určena hodnota prvního členu $a_1$ a další členy jsou definovány vzorcem $a_n=f(a_{n-1})$, kde $f$ je daná funkce. Prozkoumejme takovou posloupnost, kde $a_1=3$ a funkce $f$ je dána předpisem $f(x)={x+1\over x-1}$. Dokážete najít hodnoty $a_n$ pro $n=6,100,501$?Řešení
Párování karet
Vezmeme dva balíčky 52 karet na whist a každý zamícháme. Karty z jednoho balíčku postupně rozložíme do řady vedle sebe a pak pod tuto řadu stejným způsobem vytvoříme řadu karet z druhého balíčku. Jaký je průměrný počet dvojic stejných karet pod sebou?Řešení
Dvě tětivy
V kružnici $k$ zvolíme dvě tětivy $AB$, $DE$ tak, že tětiva $DE$ protíná tětivu $AB$ v jejím středu $C$. Nad tětivou $DE$ sestrojíme půlkružnici vně kružnice $k$ a na této půlkružnici sestrojíme bod $F$ tak, že přímky $CF$ a $DE$ jsou navzájem kolmé.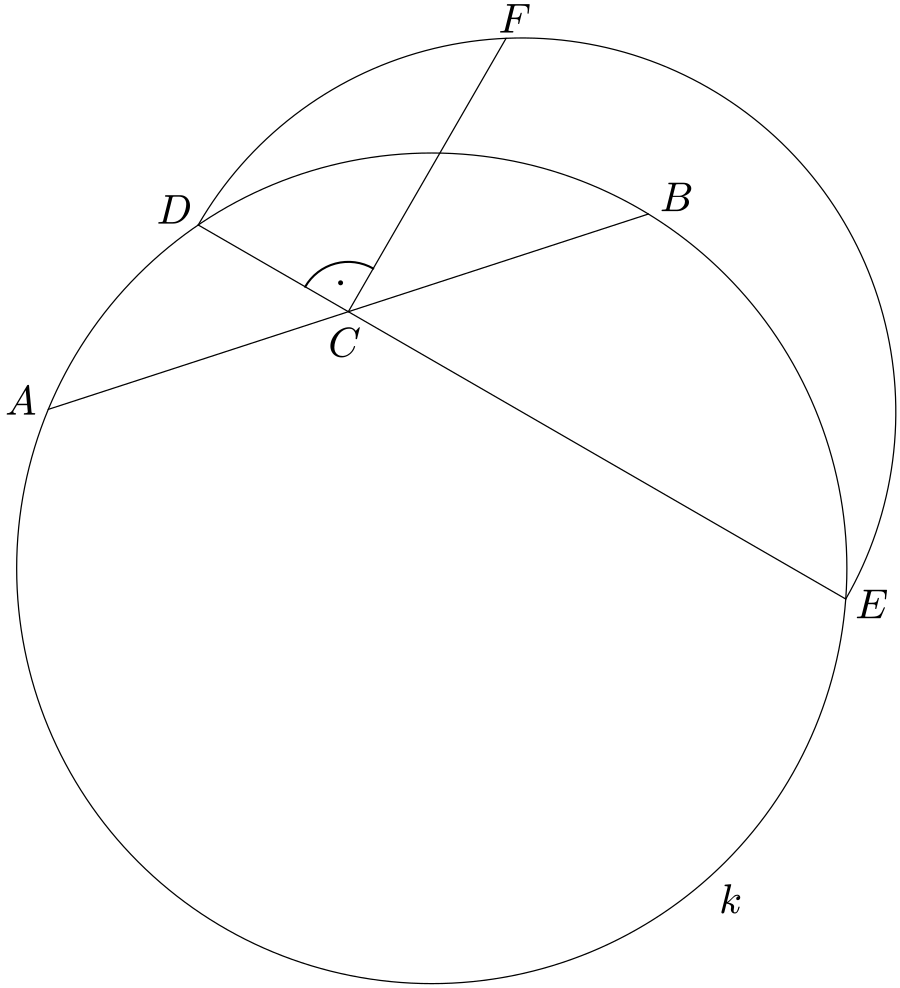
Řešení
Test z matematiky
V médiích se často setkáváme se zprávami, v nichž jsou kvantitativní údaje podávány rozdílnými způsoby, takže může být na první pohled obtížné je porovnávat. Možná je to kvůli snaze o stylovou různorodost textu, možná prostě z neporozumění. Příkladem může být následující zpráva: Skupina studentů psala písemný test z matematiky. Test se skládal z deseti úloh, za každou z nich mohl student dostat určitý počet bodů, které se nakonec sečetly. Pro úspěch ve zkoušce bylo třeba dosáhnout alespoň určitého daného počtu bodů. Po vyhodnocení testu se ukázalo, že průměrný počet bodů všech studentů byl 53, průměrný počet bodu dosažených studenty, kteří ve zkoušce uspěli, byl 65, zatímco průměrný počet bodů těch studentů, kteří neuspěli, byl 35. Ta základní informace, kolik procent studentů v testu uspělo, zůstala utajena. Dokážete ji z daných údajů odvodit?Řešení
Házení kostkou
Házíme kostkou tak dlouho, dokud součet všech hozených bodů nepřesáhne 12. Jaký bude nečastější dosažený součet přesahující 12?Řešení
Kruhová deska
Truhlář má k dispozici desku ve tvaru čtyřúhelníku, jehož dvě sousední strany mají délku 120 cm, druhé dvě sousední strany mají délku 180 cm a větší úhlopříčka má délku 200 cm. Chce z ní vyříznout co největší kruhovou desku na stůl. Kde bude střed kruhové desky a jaký bude její průměr?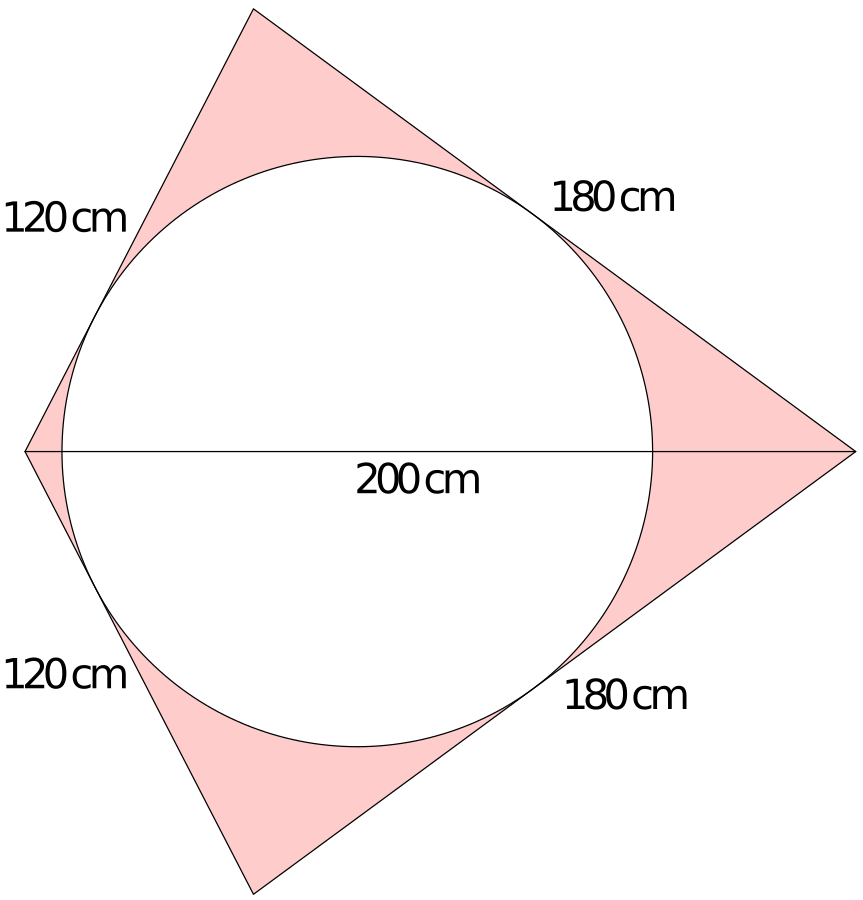
Řešení
Poslední dvě číslice čísla $11^{10}-1$
Umíte určit poslední dvě číslice čísla $11^{10}-1$? A uměli byste to v případě čísla $11^n-1$, kde $n\ge2$ je dané přirozené číslo?Řešení
Hra s kuličkami
Zahrajme si následující hru. Ve velkém džbánu je 75 bílých a 150 černých kuliček. V misce vedle máme zásobu dalších černých kuliček. Pravidla hry jsou taková, že ze džbánu vždy náhodně vytáhneme dvě kuličky a postupujeme podle toho, jaké kuličky jsme vytáhli:- (1) Jsou-li obě kuličky černé, jednu kuličku vrátíme a druhou dáme do misky.
- (2) Je-li jedna kulička černá a druhá bílá, černou kuličku dáme do misky a bílou vrátíme do džbánu.
- (3) Jsou-li obě kuličky bílé, dáme obě do misky a do džbánu přidáme jednu černou kuličku z misky.
Řešení
Rovnostranný trojúhelník ve čtverci
Ve čtverci $ABCD$ sestrojíme při straně $AB$ rovnoramenný trojúhelník $ABE$ s patnáctistupňovými úhly při vrcholech $A$, $B$.
Řešení
Kuličky
Obchodník si objednal kuličky na hraní: 19 sad o stejném počtu hliněnek a 3 sady o stejném počtu duhovek. Krabici se zásilkou bohužel otevřel až druhý den a zjistil, že dodavatel všechny kuličky, celkem 224, jednoduše nasypal do krabice. Kolik kuliček má být v každé sadě hliněnek a v každé sadě duhovek?Řešení
Kolikrát musíme hodit kostkou, aby padla šestka?
Každý, kdo hrál Člověče nezlob se, asi zažil zoufalou situaci, kdy šestka ne a ne padnout. Kdybychom si po mnoho her zapisovali, po kolikátém hodu padla šestka, a z těchto počtů hodů vypočítali průněr, k čemu bychom došli?Řešení
Vyřezávání kruhů
Truhláři zbyla kruhová deska o poloměru 1 m. Chtěl by z ní vyříznout tři nebo čtyři menší stejně velké kruhové desky na stoličky tak, aby odpad byl co nejmenší.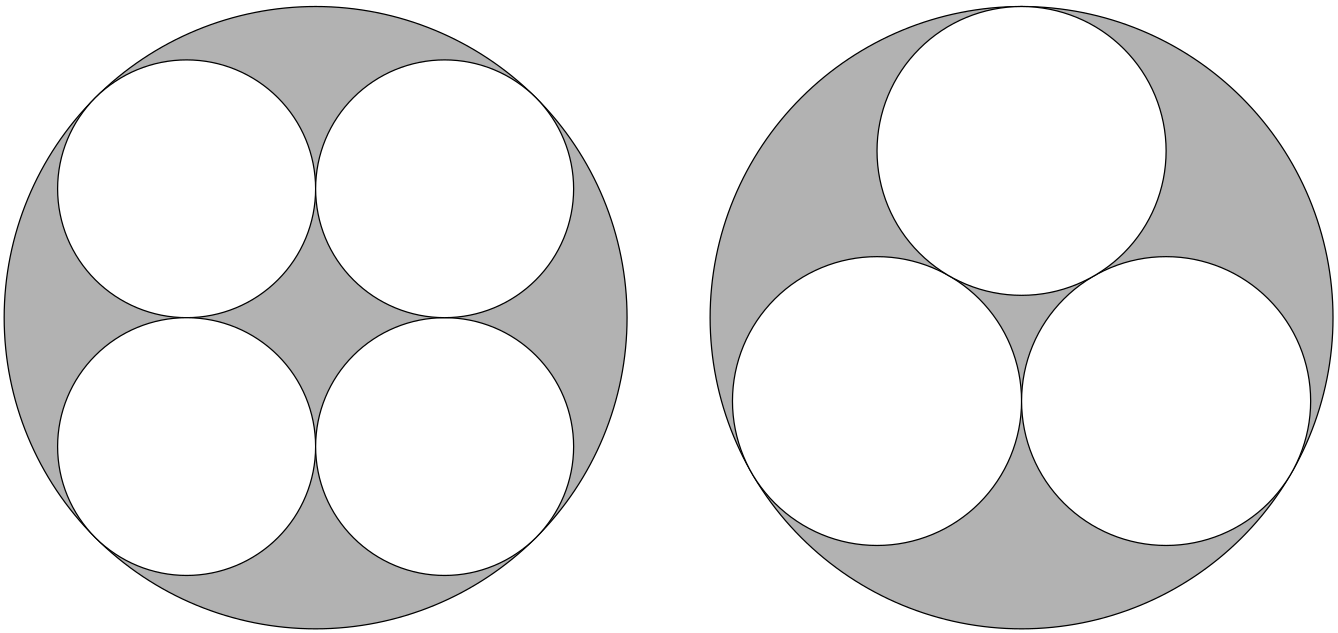
Řešení
Porota
Je třeba rozhodnout, který ze dvou soutěžících je lepší. K dispozici jsou dva porotci Karel a Lída, z nichž každý je natolik kvalifikovaný, že vítěze dokáže určit správně s pravděpodobností $p$. Aby byl vyloučen nerozhodný výsledek hlasování, přidají do poroty Martina, který však kvalifikovaně rozhodnout nedokáže, a proto si hodí korunou. Nebylo by v takovém případě lepší, kdyby o vítězi rozhodl Karel sám?Řešení
Co je větší?
Rozhodnout, které z čísel $a^b$ a $b^a$ je větší, je v některých případech snadné, např. pro $a=2$ a $b=3$. V případě, že se čísla $a$, $b$ příliš neliší, to tak snadné být nemusí. Jak je tomu v případě $a=\pi$, $b=e$, kde $e$ je Eulerova konstanta (základ přirozeného logaritmu).Řešení
Kolmé tětivy
V kružnici jsou dány dvě tětivy $AC$, $BD$, které se protínají pod pravým úhlem v bodě $F$. Bod $E$ je patou výšky v trojúhelníku $AFD$ spuštěné z bodu $F$. Bod $G$ je průsečíkem přímek $BC$, $EF$. Dokažte, že bod $G$ je středem úsečky $BC$.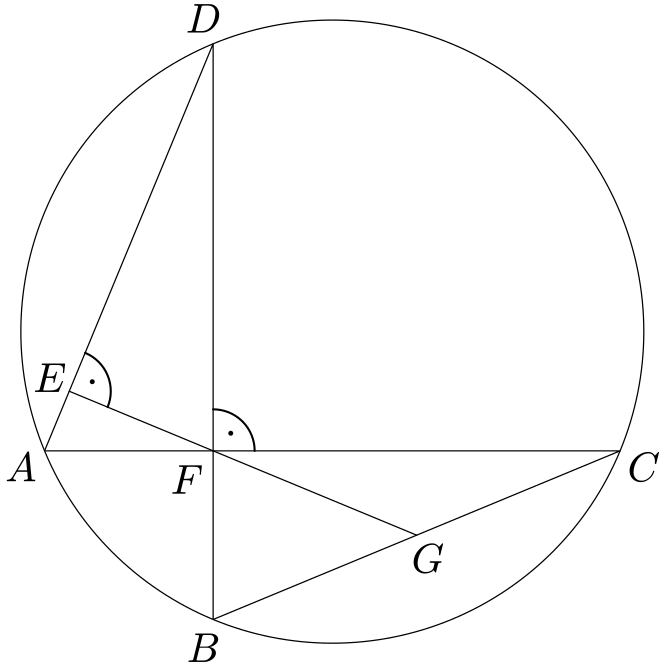
Řešení
Funkce sinu a kosinu
Nechť $f$ je taková reálná funkce, že pro všechna reálná $x$ platí $f(\cos x)=\cos17x$. Dokažte, že pak pro všechna reálná $x$ platí také $\sin17x=f(\sin x)$.Řešení
Jednobarevný list
Bridž nebo whist se hraje s $52$ kartami složenými ze čtyř sledů $13$ karet v některé ze čtyř barev. Před deseti lety proběhla světem zpráva, že v britské obci Kineton se hráčům whistu stala neuvěřitelná věc: karty byly mezi hráče rozdány tak, že každý z nich měl čistou sérii všech $13$ karet jedné barvy. To je velmi, opravdu velmi nepravděpodobná událost. Zkuste vypočítat, jaká je pravděpodobnost rozdání, kdy jen rozdávající hráč dostane celou sérii $13$ karet v jedné barvě.Řešení
Trojúhelník, kružnice a čtverec
Do rovnostranného trojúhelníku je vepsána kružnice a do ní čtverec.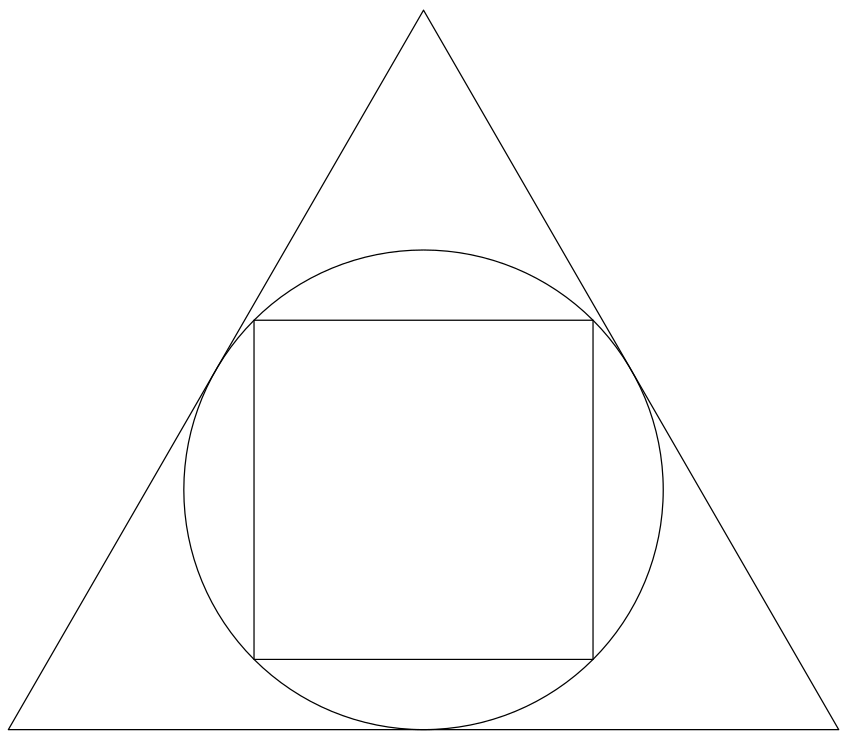
Řešení
Pět čísel
Lze najít pět přirozených čísel takových, že žádná jejich podskupina nedá v součet dělitelný pěti? (Např. čísla $1$, $3$, $8$, $11$, $13$ nevyhovují, protože $1+3+11=15=5\cdot3$.)Řešení
Normální uchazeč ještě jinak
Jsou tři druhý lidí: jedni mluví za všech okolností pravdu, jiní vždy lžou a ti zbývající jsou normální – někdy mluví pravdu a někdy lžou. Podivín, který nedůvěřuje lhářům ani pravdomluvným a nemá rád lidi, kteří zbytečně mnoho mluví, znovu hledá tajemníka, protože nebyl spokojen s výsledkem prvního ani druhého konkursu. Zkusil to ještě jednou s náročnějším požadavkem: Uchazeč musí jediným výrokem prokázat, že je normální, zároveň však nesmí být poznat, je-li výrok pravdivý nebo nepravdivý. Jak zní takový výrok?Řešení
Rovnoběžník a čtverce
Ke každé straně rovnoběžníku $ABCD$ je sestrojen čtverec: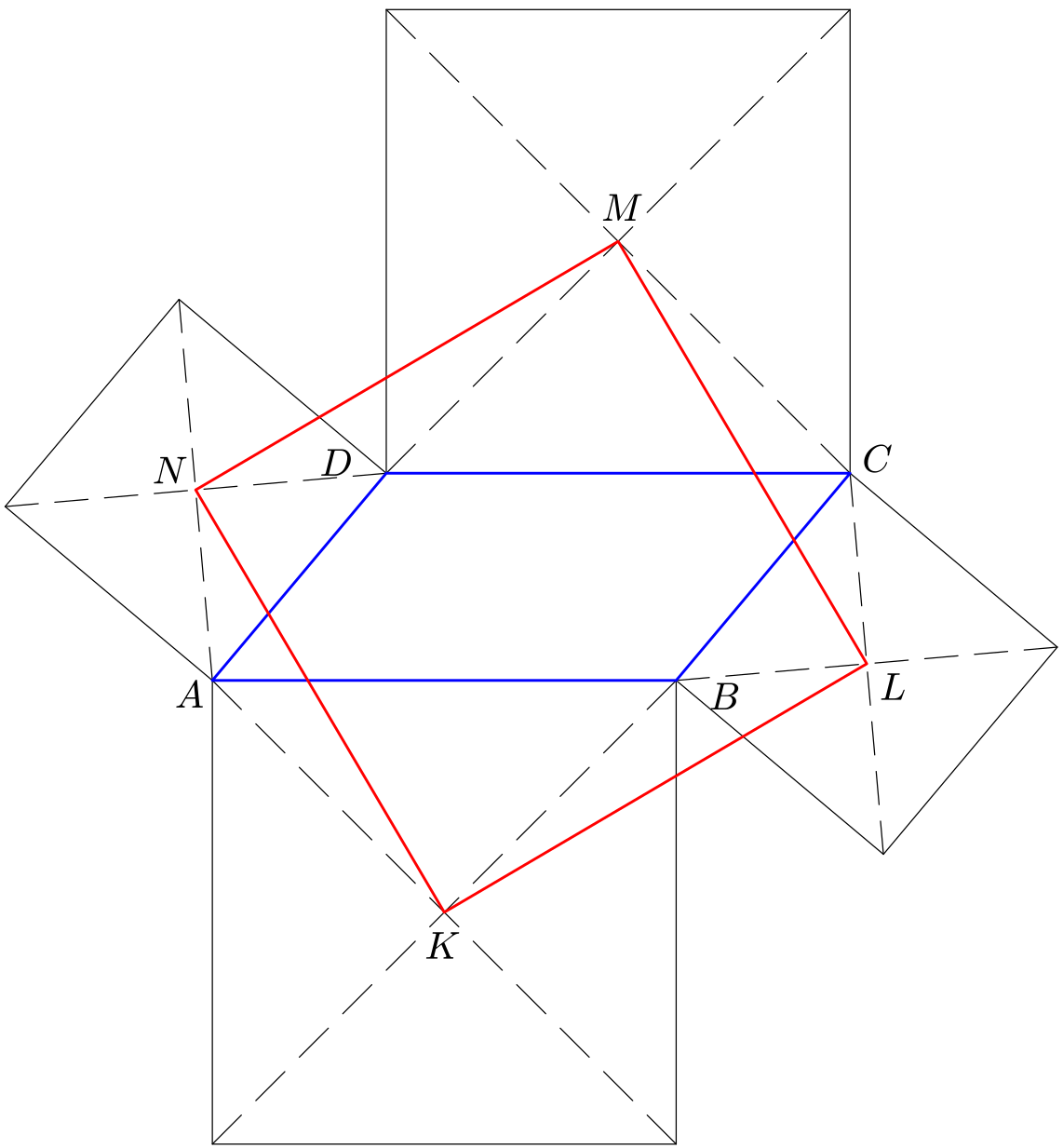
Řešení
Čísla jako součty
Přirozené číslo $3$ lze vyjádřit jako součet přirozených čísel čtyřmi různými způsoby, pokud rozlišujeme součty lišící se pořadím různých sčítanců: $3$, $2+1$, $1+2$, $1+1+1$. Kolika způsoby lze takto vyjádřit přirozené číslo $n$?Řešení
Podivný paradox
Tři vězni, Krátký, Levý a Malý se dohodli, že požádají o předčasné ukončení trestu. Všichni tři byli odsouzeni za lehké přečiny a všichni se chovali ve vězení dobře, takže všichni tři mají stejnou šanci, že jejich žádosti bude vyhověno. Dozorce vězňům řekl, že soud rozhodl o propuštění dvou z nich, ale pokud by se ho některý z vězňů zeptal, zda bude propuštěn právě on, nesmí mu odpovědět. Vězeň Krátký zvažuje, že by se mohl zeptat, který z ostatních dvou bude propuštěn. Dochází však k paradoxnímu závěru, že by se tak o sobě mohl dozvědět ještě méně, než když se ptát nebude. Uvažuje totiž následujícím způsobem. Pravděpodobnost, že bude propuštěn, je $2\over3$, protože jsou tři možnosti – propuštěni budou buď Krátký a Levý, nebo Krátký a Malý, nebo Levý a Malý. Dva ze tří případů jsou pro něj příznivé. Když mu však dozorce řekne, že bude propuštěn Levý, pak jsou dvě možnosti: propuštěn bude Levý a Krátký, nebo Levý a Malý. Pro Krátkého je zde příznivá jedna ze dvou možností, každá s pravděpodobností $1\over2$, což je méně než $2\over3$. To je však podivné. Je možné, aby se Krátkého vyhlídky po získání doplňující informace zhoršily?Řešení
Zajímavé vztahy v trojúhelníku
V trojúhelníku $ABC$ označme $D$ patu výšky na stranu $AB$ a na úsečce $DC$ zvolme bod $E$.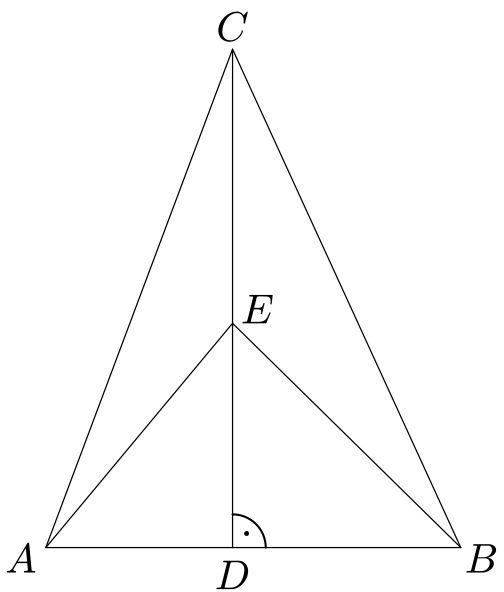
Jaký vztah platí, když bod $E$ leží na přímce $CD$ vně úsečky $CD$?
Řešení
Normální uchazeč jinak
Jsou tři druhý lidí: jedni mluví za všech okolností pravdu, jiní vždy lžou a ti zbývající jsou normální – někdy mluví pravdu a někdy lžou. Podivín, který nedůvěřuje lhářům ani pravdomluvným a nemá rád lidi, kteří zbytečně mnoho mluví, opět hledá tajemníka, protože s výsledkem předchozího konkursu nebyl spokojen. Tentokrát do inzerátu napsal, že uchazeč musí nejmenším možným počtem nepravdivých výroků prokázat, že je normální. Kolik takových výroků stačí?Řešení
Jak se má mladý goista rozhodnout?
Otec a jeho syn chodí do klubu hrát go. Otec chce syna povzbudit k dalšímu rozvoji v hře. Nabídne mu odměnu, když vyhraje alespoň dvě partie po sobě v sérii tří partií hraných střídavě proti otci a proti Adamovi, který je nejsilnějším hráčem v klubu, přičemž si může vybrat ze dvou možností: v první a třetí partii bude jeho soupeřem buď otec, nebo Petr. Kterou z nabízených možnosti si má syn vybrat?Řešení
Dva rovnoběžníky
V rovině jsou dány dva rovnoběžníky $ABCD$, $AEFG$, o kterých víme jen to, že bod $E$ leží uvnitř strany $CD$ a bod $B$ leží uvnitř strany $EF$.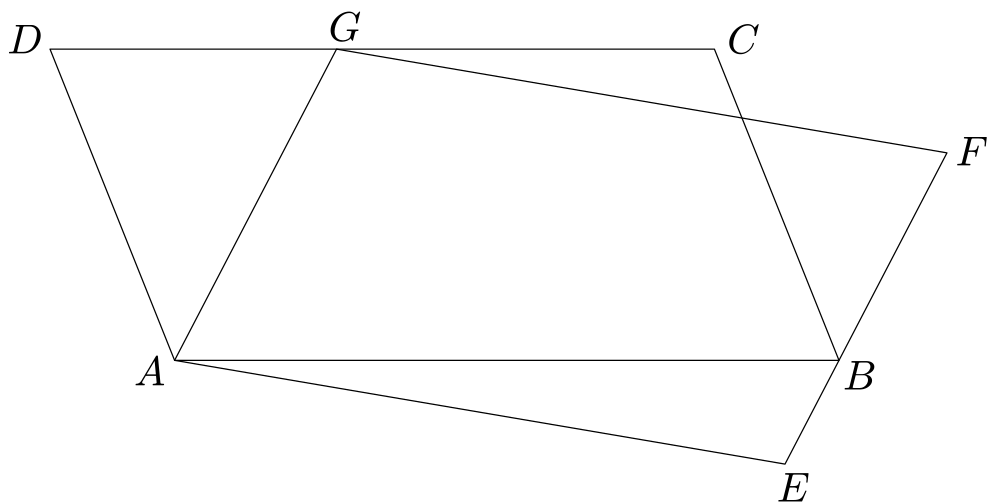
Řešení
Je dán součet a součin dvou čísel
Součet dvou čísel je 2, jejich součin je 3. Určete součet převrácených hodnot těchto dvou čísel.Řešení
Oříšky v čokoládě
Eva je doma v karanténě a snaží se dohnat zameškanou látku ze školy. Mlsá při tom oříšky obalené v černé a bílé v čokoládě. Protože právě studuje pravděposodobnost, napadají ji otázky:- (1) Je možné, že s pravděpodobností přesně ${1\over2}$ budou první dva oříšky bílé?
- (2) Jaký nejmenší počet oříšků v pytlíku musí být, aby taková situace mohla nastat?
- (3) Jaký nejmenší počet oříšků v pytlíku musí být, aby taková situace mohla nastat, je-li v něm sudý počet černých oříšků?
Řešení
Trojúhelník a n-tá odmocnina
Je dán trojúhelník o stranách délek $a$, $b$, $c$. Pak pro každé přirozené číslo $n$ platí, že úsečky délek $\root n \of a$, $\root n \of b$, $\root n \of c$ také tvoří trojúhelník. Zkuste to dokázat. Platí obdobné tvrzení i pro mocniny délek stran?Řešení
Trojúhelníková síť
V rovině je dáno $n\ge3$ bodů, z nichž žádné tři neleží v přímce. Dokažte, že pak existuje alespoň ${1\over6}n(n-1)$ trojúhelníků s vrcholy v daných bodech, které neobsahují žádný další z daných bodů.Řešení
Normální uchazeč
Jsou tři druhý lidí: jedni mluví za všech okolností pravdu, jiní vždy lžou a ti zbývající jsou normální – někdy mluví pravdu a někdy lžou. Podivín hledá tajemníka. Nedůvěřuje lhářům ani pravdomluvným, nemá rád lidi, kteří zbytečně mnoho mluví, a také chce, aby tajemník nebyl hloupý. Proto do inzerátu napsal, že uchazeč musí nejmenším možným počtem pravdivých výroků prokázat, že je normální. Kolik takových výroků mu stačí?Řešení
Dělení trojúhelníkové parcely jinak
Trojúhelníková parcela $ABC$ o obsahu $30\,{\rm ha}$ je rozdělena dvěma přímými hranicemi $CD$ a $AE$ na čtyři části: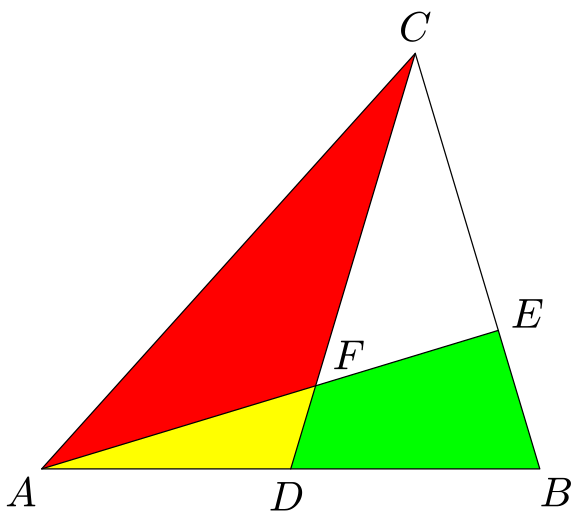
Řešení
Je číslo $7251^5+6159^7$ dělitelné $90$?
Dokážete odpovědět bez použití kalkulačky nebo bez úmorného počítání?Řešení
Ukradená husa podruhé
Už jsme tu měli vesnici, kde žijí dva typy lidí: poctivci, kteří vždy mluví pravdu, a lháři, kteří vždy lžou. Není však jisté, kdo je kdo. Někdo sousedovi ukradl husu. Starosta chce zjistit, kdo to byl, a protože nemá rád dlouhé řeči, požaduje, aby se každý na svou obhajobu vyjádřil jednou větou. Honza Dlouhý je podivín, který nemá rád poctivce. Sám není poctivec, ale husu neukradl. Záleží mu na tom, aby starostu přesvědčil nejen o své nevině, ale také o tom, že nepatří mezi ty jím opovrhované poctivce. Jak to provede?Řešení
Překládáme čtverec
Vezmeme papír tvaru čtverce o straně 20 cm a přeložíme ho tak, že jeden z vrcholů umístíme do středu protější strany. Jeden roh pak bude přečnívat. Jak velký bude plošný obsah přečnívajícího trojúhelníku, který je na obrázku vybarven červeně?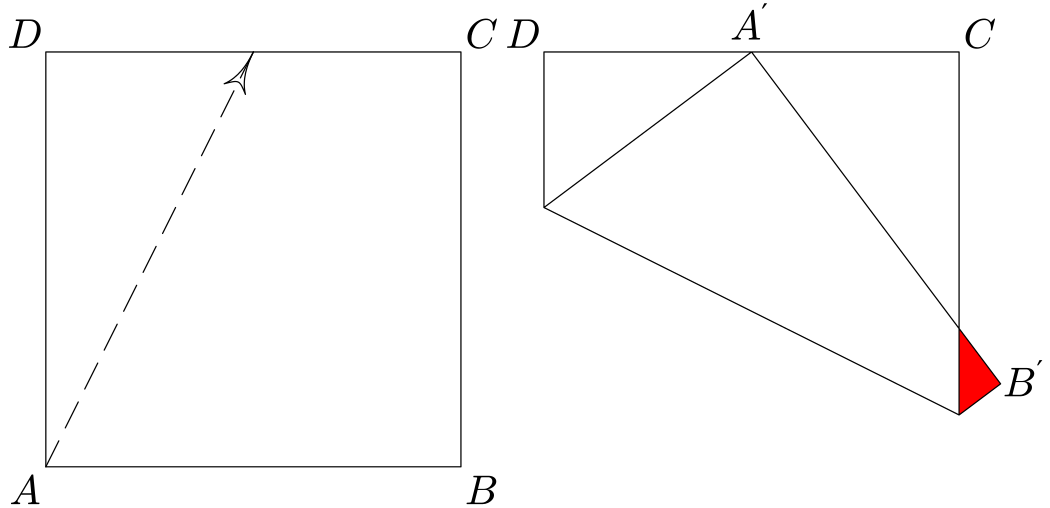
Řešení
Trik s hodinami a kostkou
Kouzelník s čísly dá vybranému diváku hodinový ciferník, hrací kostku, papír a tužku. Otočí se k němu zády a vyzve ho, aby si zvolil číslo od jedné do dvaceti, hodil kostkou a kostku položil na to číslo na ciferníku, které padlo na kostce. Pak divák projde ciferník postupně po jednotlivých číslech ve směru hodinových ručiček, přičemž počet kroků je dán jím zvoleným číslem. Číslo na ciferníku, do kterého dojde, si poznamená. Potom udělá totéž v opačném směru. Obě výsledná čásla sečte a výsledek oznámí kouzelníkovi. Ten bleskurychle řekne číslo, které padlo na kostce. Jak to dokáže?Řešení
Ani lhář ani poctivec
Představte si, že žijete ve vesnici, kde jsou tři typy lidí: poctivci, kteří se chovají vždy čestně a vždy mluví pravdu, lháři, kteří páchají nepravosti a vždy lžou, a normální lidé, kteří lžou jen občas. Není však jisté, kdo je kdo. Jste normální a máte za úkol o tom přesvědčit jedinou větou. Co řeknete?Řešení
Co je větší?
V obdélníku $ABCD$ zvolíme bod $X$ uvnitř strany $AD$ a bod $Y$ uvnitř strany $CD$. Úsečky $AY$, $BY$, $XB$, $XC$ rozdělují obdélník na osm částí. Co má větší obsah – červeně vybarvená nebo zeleně vybarvená část?
Řešení
Čarování s čísly
Tohle už vážně vypadá jako čarování. Kouzelník s čísly předá divákovi kartu s deseti řádky očíslovanými od 1 do 10. Otočí se k němu zády a požádá ho, aby do prvních dvou řádků zapsal nějaká dvě celá čísla mezi 1 a 20 a pak do každého dalšího řádku zapsal součet čísel z předchozích dvou řádků. Pak si nechá kartu ukázat a požádá diváka, aby sečetl všech deset zapsaných čísel. Karta vypadá třeba takto:
| 1 | 13 | |
| 2 | 4 | |
| 3 | 17 | |
| 4 | 21 | |
| 5 | 38 | |
| 6 | 59 | |
| 7 | 97 | |
| 8 | 156 | |
| 9 | 253 | |
| 10 | 409 |
Řešení
Ukradená husa
V jedné vesnici žijí dva typy lidí: poctivci, kteří vždy mluví pravdu, a lháři, kteří vždy lžou. Není však jisté, kdo je kdo. Někdo sousedovi ukradl husu. Starosta chce zjistit, kdo to byl, a protože nemá rád dlouhé řeči, požaduje, aby se každý na svou obhajobu vyjádřil jednou větou. Josefu Broučkovi záleží na tom, aby starostu přesvědčil nejen o své nevině, ale také o tom, že není lhář. Jak to provede?Řešení
Kružnice a trojúhelník
V rovině je dána kružnice $k$. Sestrojte trojúhelník $ABC$ těchto vlastností:- (1) Přímka $AC$ je tečnou kružníce $k$.
- (2) Kružnice $k$ je opsána trojúhelníku $ABD$, kde $D$ je střed strany $BC$.
- (3) Úsečka $AC$ je dvakrát delší než úsečka $AD$.
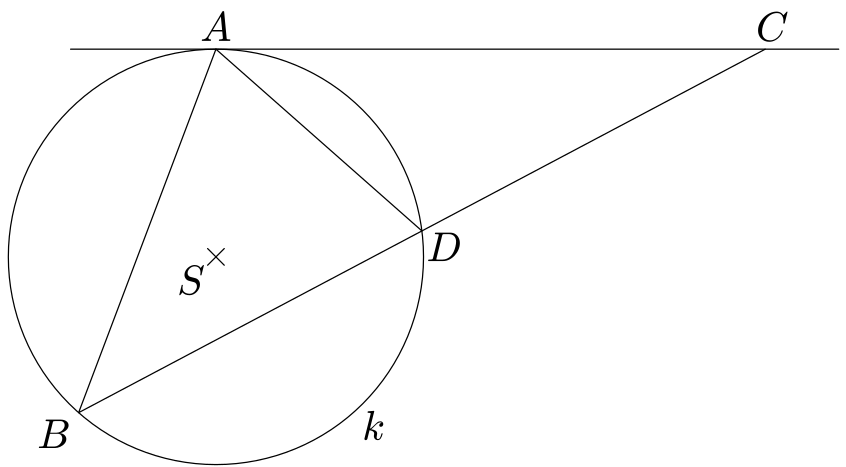
Řešení
Ještě jednou kouzelné číslo 1089
Již jsme tu viděli, že číslo $1089$ má "kouzelné" vlastnosti. Ukážeme další. Kouzelník vybere mezi diváky dobrovolníka a požádá ho, aby číslo $1089$ vynásobil jakýmkoli trojciferným číslem, které neprozradí. Pak se ho zeptá, kolik číslic má výsledek. Pak ho požádá, aby si vybral libovolnou číslici a kouzelníkovi vyjmenoval ty zbývající. Kouzelník mu pak řekne, jaká je ta zbylá číslice, nebo nabídne dvě číslice, z nichž jedna to určitě je. Magie?Řešení
Lhář se obhajuje
Na podivném ostrově žijí jen poctiví lidé, kteří se chovají vždy čestně a vždy mluví pravdu, a lháři, kteří páchají nepravosti a vždy lžou. Je však těžké je rozlišit. Komisař vyšetřující zločin vyslýchá jednoho z podezřelých. Vyslýchaný, kterým je shodou okolností lhář (což ovšem komisař neví), je nevinen. Má možnost přesvědčit komisaře o své nevině jedinou větou. Jak ta věta zní?Kdyby vyslýchaný byl vinen, měl by také možnost jedinou větou přesvědčit komisaře o své nevině?
Řešení
Vrcholy pravoúhlých trojúhelníků
V rovině je dána úsečka $AB$. Najděte množinu všech vrcholů pravoúhlých trojúhelníků $XYZ$ těchto vlastností:- (1) Přepona $XY$ je částí úsečky $AB$.
- (2) Pro délky odvěsen platí $|XZ|=|AX|$, $|BZ|=|BY|$.
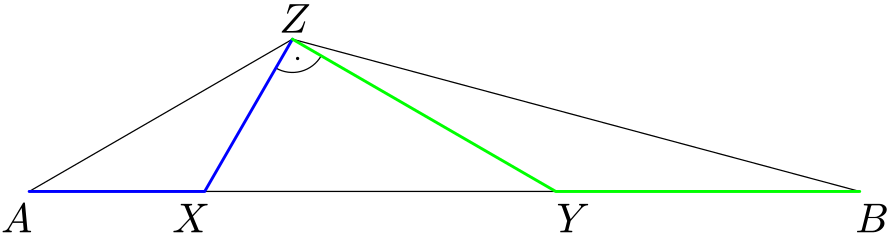
Řešení
Kouzelné číslo 1089
Číslo $1089$ má "kouzelné" vlastnosti. Kouzelník s čísly vybere mezi diváky dobrovolníka, dá mu papír a tužku, otočí se k němu zády a požádá ho, aby napsal nějaké trojciferné číslo, jehož číslice zleva doprava klesají, a od tohoto čísla odečetl číslo tvořené stejnými číslicemi v opačném pořadí. Pak ho požádá, aby k výsledku přičetl číslo tvořené stejnými číslicemi jako výsledek, ale v opačném pořadí. Pak sáhne do klobouku, vytáhne lístek s číslem 1089 a ukáže ho obecenstu. Pokud dobrobvolník počítal správně, překvapeně potvrdí, že právě to je výsledkem jeho výpočtu. Jak je to možné?Řešení
Obhajoba lháře či poctivce
Na podivném ostrově žijí jen poctiví lidé, kteří se chovají vždy čestně a vždy mluví pravdu, a lháři, kteří páchají nepravosti a vždy lžou. Je však těžké je rozlišit. Komisař vyšetřující zločin vyslýchá jednoho z podezřelých. Vyslýchaný je nevinen a má možnost o tom přesvědčit komisaře jedinou větou. Jak ta věta zní?Řešení
Mnohostěn
Tato úloha vyžaduje jistou prostorovou představivost. Úkolem je najít nejmenší přirozené číslo $n$ takové, že v prostoru existuje konvexní mnohostěn s těmito vlastnostmi:- (1) Mnohostěn má $n$ hran.
- (2) Mnohostěn má alespoň $10$ vrcholů.
- (3) Každé dva vrcholy mnohostěnu lze propojit alespoň čtyřmi cestami, z nichž žádné dvě nemají žádné společné vrcholy kromě počátku a konce.
Řešení
30 bonbónů
Maminka má pytlík se 30 bonbóny. Jak je rozdělí rovným dílem mezi pět děti tak, aby 6 bonbónů zůstalo v pytlíku?Řešení
Koho obvinit?
Před soudem stojí tři obžalovaní z loupežného přepadení: Tlustý, Ušatý a Vysoký. Z vyšetřování vyplynulo, že:- (1) Pokud loupež neprovedl Tlustý nebo ji provedl Ušatý, pak se jí zúčastnil i Vysoký.
- (2) Pokud loupež neprovedl Tlustý, pak ji neprovedl ani Vysoký.
Řešení
Dělení trojúhelníkové parcely
Trojúhelníková parcela $ABC$ o obsahu $10\,{\rm ha}$ je rozdělena dvěma přímými hranicemi $CD$ a $AE$ na čtyři části: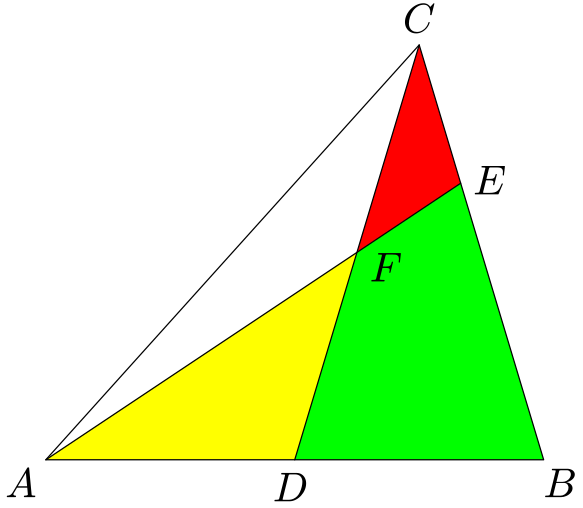
Řešení
Kočky
Bez dlouhého přemýšlení odpovězte, kolik koček je ve čtvercové místnosti, když v každém rohu sedí jedna kočka, proti každé kočce sedí tři kočky a na ocase každé kočky sedí kočka?Řešení
Kdo je lupič?
Policie zadržela tří známé recidivisty Ptáčka, Raroha a Slavíka podezřelé z loupeže. Je prokázáno, že loupež musel provést někdo z nich. Policejní komisař shrnul poznatky z vyšetřování:- (1) Pokud loupež provedl Ptáček a Raroh je nevinen, pak loupež provedl Slavík.
- (2) Slavík nikdy nepracuje sám.
- (3) Ptáček nikdy nepracuje se Slavíkem.
Řešení
Kružnice ve čtvercové síti
Karel zahání dlouhou chvíli rýsováním kružnic na čtverečkovaném papíru, které mají střed ve vrcholu některého čtverce a poloměr rovný celočíselnému násobku velikosti strany čtverce. Po narýsování několika kružnic se mu zdá, že když bude poloměr dost velký, může kružnice procházet středem některého ze čtverců sítě.
Řešení
Ciferný součet
Před časem jsme v jedné z úloh připomněli historku, podle které pozdější slavný matematik Carl Friedrich Gauss v dětství zaskočil svého učitele bleskovým sečtením čísel od $1$ do $100$. Přijdete na to, jak rychle sečíst všechny číslice, ze kterých jsou sestavena čísla od $1$ do $1\,000\,000$?Řešení
Ostrov pravdomluvných, lhářů a normálních
Představme si ostrov, kde každý z domorodců je buď vždy pravdomluvný, nebo vždy lže, nebo je normální, tj. někdy mluví pravdu, někdy lže. Jeden z domorodců byl předvolán k náčelníkovi pro podezření, že zločin spáchal. Přísná kmenová tradice vyžaduje, aby se obviněný obhájil jediným výrokem. Ví se, že pachatelem je lhář. Obviněný je lhář, ale náčelník to o něm neví. Co má říci obviněný, aby náčelníka přesvědčil o své nevině?Řešení
Paradoxní skládačka popáté
Již jsme tu měli řadu zdánlivých paradoxů, kdy rozložením obrazce na několik menších a opětovným složením jsme dostali obrazec, jehož obsah se od původního lišil o jednotku. Rozdíl však může být i větší, např. $2$ jednotky: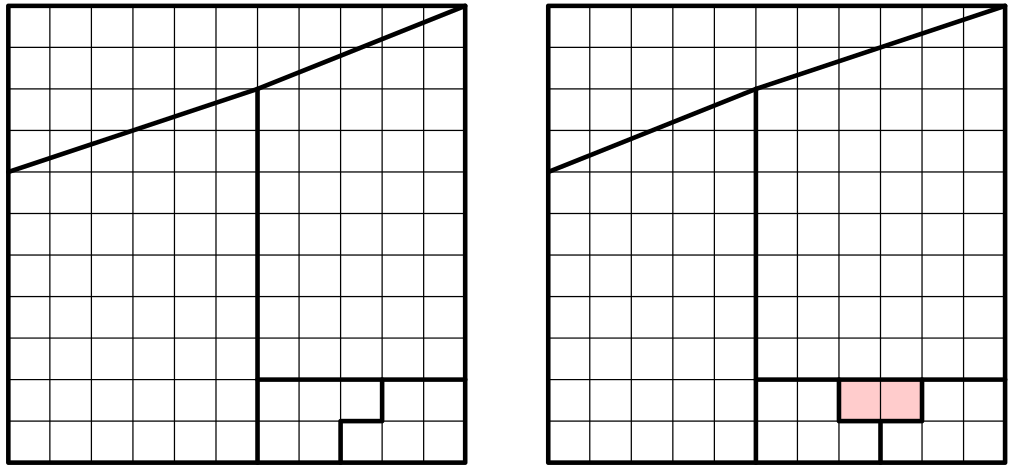
Řešení
„Magický“ trojúhelník
Čísla $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9$ rozmístěte kolem rovnostranného trojúhelníku tak, že u každého vrcholu bude jedno, u každé strany mezi vrcholy budou další dvě a bude platit, že součet každé čtveřice čísel při straně trojúhelníku se bude rovnat $20$.Řešení
Nařízení hodin
Pavel rád tráví čas na chalupě uprostřed lesa, kam není zaveden elektrický proud. Jediné hodiny, které tam má, se zastavily a ke všemu se mu vybil mobilní telefon. Pavel zašel na kraj lesa, odkud je vidět na věž kostela ve vesnici, zjistil, kolik je hodin, hned se vrátil a nařídil správně své hodiny. Jak to udělal, když nemohl změřit, jak dlouho mu trvala cesta? (Předpokládáme, že tam i zpět šel stejně rychle.)Řešení
Rozdělení obdélníkové desky
Na obdélníkové desce o rozměrech $4\,{\rm m}\times3\,{\rm m}$ je vyryta úhlopříčná rýha. Úkolem je rozříznout ji dvěma řezy na čtyři obdélníkové díly podle náčrtu tak, aby žlutě vyznačené díly měly dohromady co největší obsah a přitom nebyly poškozeny rýhou.
Řešení
24 bonbónů
Maminka dala třem dětem $24$ bonbónů s podmínkou, že každý z nich dostane stejný počet. Aby to nebylo tak jednoduché, vymyslela hru. Na jednu hromádku dala $11$ bonbónů, na druhou $7$ a na třetí zbývajících $6$. Děti mají přemistít bonbóny tak, aby jich na každé hromádce bylo $8$. Musejí však přitom dodržovat následující dvě pravidla:- V každém kroku mohou přemístit bonbóny z jedné hromádky na jinou tak, že k hromádce přidají přesně tolik bonbónů, kolik jich tam právě je.
- Za čtvrtý, pátý a každý další tah dostanou trestný bod a na konci za každý trestný bod každé dítě mamince vrátí $1$ bonbón.
Řešení
Malé „kouzlo“ s hracími kostkami
Na večírku můžete pobavit přátele malým „kouzlem“: dáte jim tři hrací kostky, otočíte se k nim zády a požádáte je, aby kostky libovolným způsobem položili vedle sebe, zapsali tři číslice označující body na horních stěnách kostek a za ně připsali tři číslice označující body na dolních stěnách kostek (pořadí číslic musí odpovídat pořadí kostek). Pak je požádáte, aby výsledné šestimístné číslo vydělili číslem $111$ a řekli vám výsledek. Na základě toho jim ihned oznámíte, jaké číslice a v jakém pořadí jsou na vrchních stranách kostek. Přijdete na to, jak a proč to funguje?Řešení
Jak vyrobit kruhovou desku
Truhlář dostal zvláštní zakázku: ze dvou desek tvaru na obrázku vyrobit jednu velkou kruhou desku na stůl. Desky mají uprostřed otvor ohraničený dvěma čtvrtkruhy o poloměru $r$, které v krajních bodech svírají pravý úhel, a jejich obvod je tvořen křivkou, jejíž každý bod má od středového otvoru vzdálenost $r$.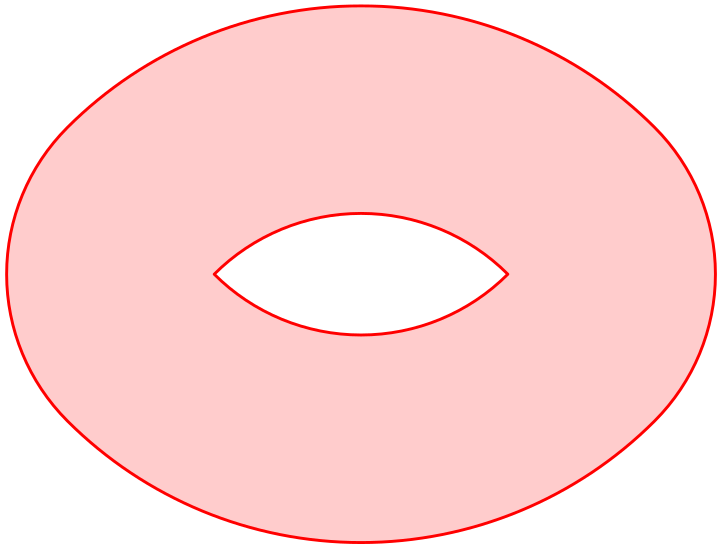
Řešení
Mocniny tří
S přirozenými čísly lze provádět různá "kouzla". Zkuste dokázat, že pro každé přirozené číslo $n$ existují taková dvě přirozená čísla $r$, $s$, že číslo $3^r-3^s$ je dělitelné číslem $n$.Tato úloha byla zařazena do přípravného kola 30. ročníku Matematické olympiády v kategorii B pro studenty středních škol.
Řešení
Zbrklá obhajoba
Policejní komisař při výslechu zadrženého člověka podezřelého z loupeže prohlásil: "Pokud jste loupež provedl, pak jste měl komplice." Podezrřelý okamžitě vyhrkl: "To není pravda!" Byla to vhodná reakce?Řešení
Paradoxní skládačka počtvrté
Jiná varianta zdánlivě paradoxního rozkladu a složení obrazce. Pravoúhlý trojúhelník s odvěsnami velikostí $5$ a $13$ na obrázku vlevo rozstřihneme na čtyři části a složíme do stejně velkého trojúhleníku, jak je naznačeno na obrázku vpravo.
Všimněte si, že rozměry obrazců opět tvoří po sobě jdoucí členy Fibonacciho posloupnosti: $1,\ 2,\ 3,\ 5,\ 8,\ 13$ (viz komentář v řešení úlohy Paradoxní skládačka podruhé).
Řešení
Kdo umyje nádobí?
Tři sourozenci, Karel, Lída a Marie se dohadují, kdo dnes po rodinném obědě umyje nádobí. Karel umíněně trvá na tom, že ho půjde mýt jen tehdy, když s ním půjde jedna ze sester, ne však obě najednou. Lída naopak vyžaduje, že na to půjdou všichni tři společně. Kdo tedy vlastně nádobí umyje?Řešení
Obarvený pětiúhelník
V konvexním pětiúhelníku obarvíme každou stranu a každou úhlopříčku buď červeně nebo modře tak, že aby žádný z trojúhelníků tvořených těmito úsečkami nebyl jednobarvený, např. takto:
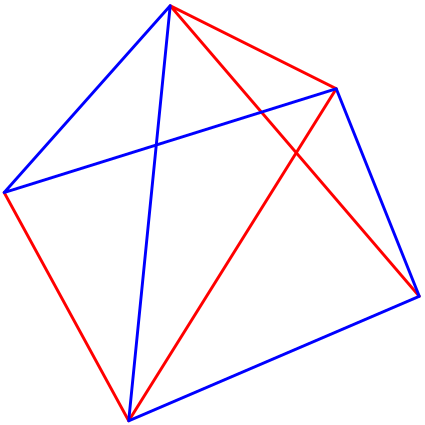
Tato úloha byla zařazena do přípravného kola 30. ročníku Matematické olympiády v kategorii C pro studenty středních škol.
Řešení
Rozklad čtverce
Ve čtverci o straně délky $1$ jsou z každého vrcholu vepsány čtvrtkružnice o poloměru $1$. Čtverec je tím rozdělen na $9$ částí.
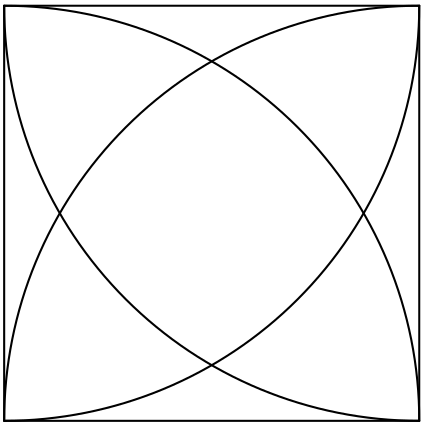
Tato úloha byla zařazena do přípravného kola 30. ročníku Matematické olympiády v kategorii C pro studenty středních škol.
Řešení
Prvočíslo a mocnina
Hledá se takové prvočíslo, že číslo o 4 větší je druhou mocninou nějakého celého čísla.Řešení
Paradoxní skládačka potřetí
Tohle je další varianta zdánlivě paradoxního rozkladu a složení obrazce. Obdélník vlevo obsahuje $8\cdot13=104$ čtverečků.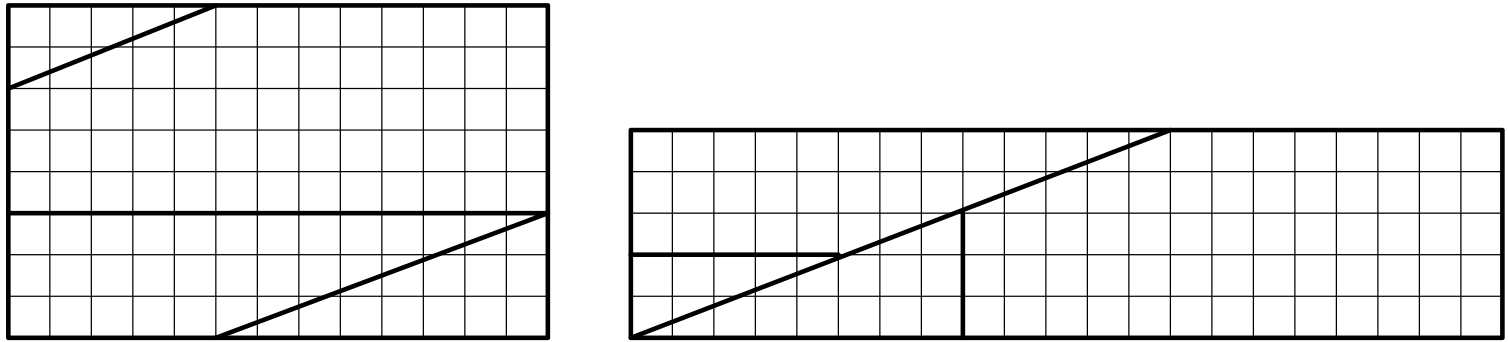
Řešení
Kdo je vrah?
Policejní komisař zatkl tři podezřelé z vraždy, Adamse, Browna a Clarka. Ze složitého vyšetřování vyplynuly dva poněkud zvláštní poznatky:- 1. Pokud Adams není vrahem nebo Brown je vrahem, pak je vrahem Clark.
- 2. Pokud Adams není vrahem, pak Clark není vrahem.
Řešení
Spěšná zásilka
Nemocnice urgentně potřebuje zásilku speciálních léků, která je k dispozici jen v hlavním městě. Léky byly odeslány letadlem na nejbližší letiště. Z nemocnince byla pro léky vyslána sanitka tak, aby na letiště dorazila právě k předpokládanému příletu letadla. Zásilku se však podařilo poslat dřívějším letem a aby byla doručena do nemocnince co nejdříve, převzala ji policie a ihned s ní vyrazila naproti sanitce. Po půlhodině se setkala se sanitkou, zásilku léků předala a sanitka ihned vyrazila zpět do nemocnice. Tak se stalo, že léky byly doručeny do nemocnice o dvacet minut dříve proti předpokladu. O kolik minut dříve přistálo letadlo s léky než to, které je mělo původně dopravit?Řešení
Rychlý odhad
Podívejte se na následující dva sloupce čísel a rychle bez pracného počítání rozhodněte, který sloupec dá větší součet.
| 123456789 | 1 | |
| 123456780 | 21 | |
| 123456700 | 321 | |
| 123456000 | 4321 | |
| 123450000 | 54321 | |
| 123400000 | 654321 | |
| 123000000 | 7654321 | |
| 120000000 | 87654321 | |
| 100000000 | 987654321 |
Řešení
Trojúhelník s nejmenším obvodem
Je dán ostroúhlý trojúhelník $ABC$ a uvnitř jeho strany $AB$ bod $K$. Najděte uvnitř strany $BC$ bod $L$ a uvnitř strany $AC$ bod $M$ tak, aby obvod trojúhelníku $KLM$ byl minimální.
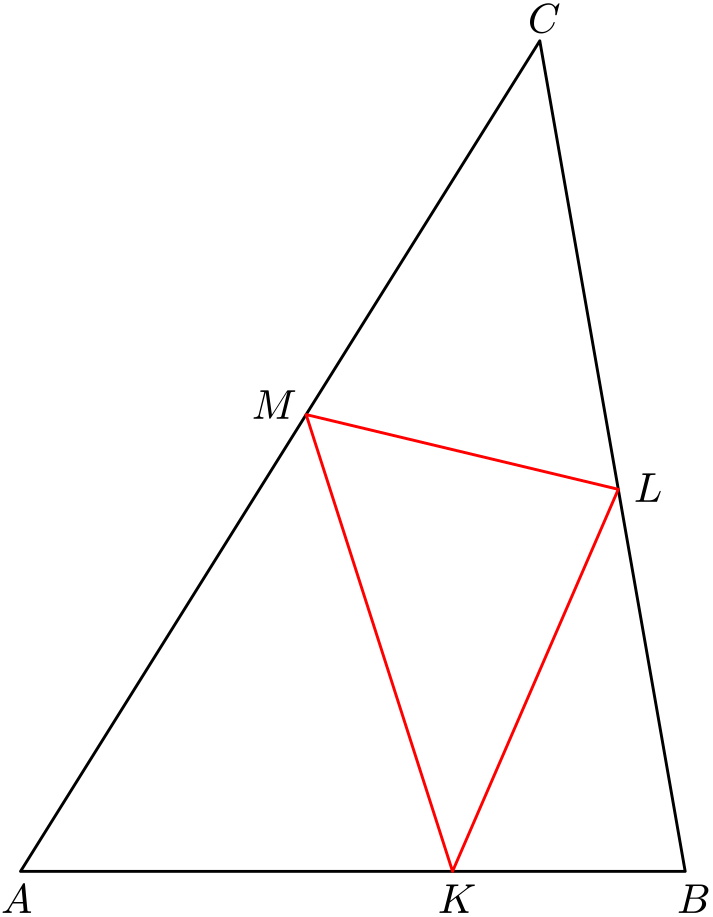
Řešení
Tři početní hlavolamy se zápalkami
Obrazce sestavené ze zápalek znázorňují tři zjevně neplatné rovnosti. Úkolem je obrazce upravit tak, aby rovnosti platily. Vlevo k tomu stačí přesunout jednu zápalku, uprostřed a vpravo stačí přesunout vždy dvě zápalky.

Řešení
Číslování hran krychle
Už jsme tu zkoušeli očíslovat hrany čtyřstěnu, teď můžeme zkusit očíslovat stěny krychle čísly 1, 2, 3, 4, 5, 6 tak, aby součet tří čísel, kterými jsou očíslovány stěny se společným vrcholem, byl pro všechny vrcholy stejný. Rovnou napovíme, že to nejde. Jak to dokázat?Úloha byla zařazena do 2. kola 30. ročníku Matematické olympiády v kategorii Z pro žáky základních škol.
Řešení
Která ze třinácti mincí je falešná?
Už jsme tu řešili několik úloh na hledání falešných mincí, např. tuto. Přestože tam byl počet mincí větší, úloha byla významně snazší, protože jsme navíc věděli, že hledáme minci, která lehčí než ostatní. Falešné mince však mohou být i trochu těžší než ty pravé. V této úloze jde o to třemi váženími na dvojramenných vahách najít mezi 13 mincemi jednu, která se od ostatních nepatrně liší svou hmotností. Mincí je tedy méně, ale chybí informace, zda je falešná mince lehčí nebo těžší.Řešení
Které číslo jsme násobili?
Trojciferné jsme vynásobili číslem $36$. Výsledek končí trojčíslím $324$. Jaké číslo jsme násobili?Řešení
Barevné tětivy
Na kružnici zvolíme 6 různých bodů a každé dva spojíme modrou nebo červenou úsečkou tak, že vznikne právě jeden červený a právě jeden modrý trojúhelník. Např. takto: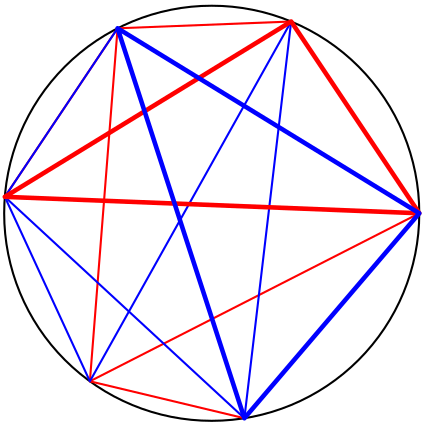
Řešení
Koule a krychle trochu jinak
Je dána krychle $ABCDEFGH$ o hraně délky $a$. Určete střed a délku poloměru $r$ kulové plochy, která protíná stěnu $BCG$ v kružnici $k$ vepsané čtverci $BCGF$ a prochází bodem $A$.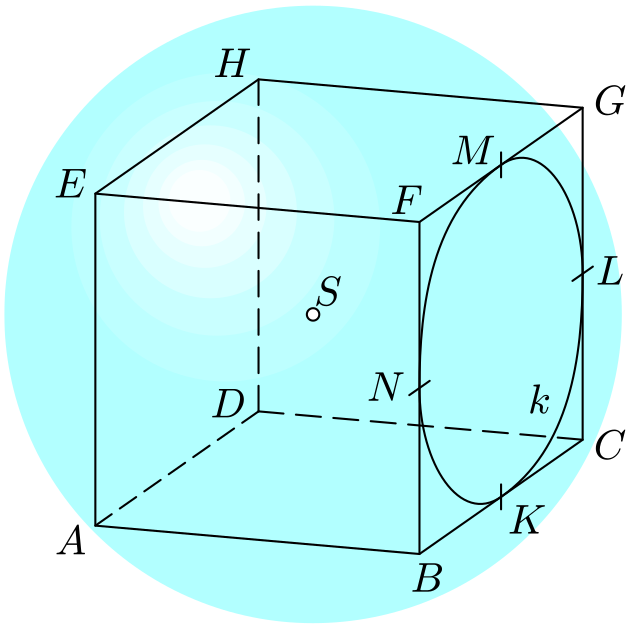
Řešení
Úlohy z minulých týdnů
Číslování hran čtyřstěnu
Chcete-li se někoho na delší dobu zbavit, dejte mu za úkol očíslovat hrany pravidelného čtyřstěnu čísly 1, 2, 3, 4, 5, 6 tak, aby součet tří čísel, kterými jsou očíslovány hrany téže stěny, byl pro všechny stěny stejný. Možná ho po několika marných pokusech napadne, že to nejde. Jak to však dokázat?Úloha byla zařazena do 1. kola 30. ročníku Matematické olympiády v kategorii Z pro žáky základních škol.
Řešení
Posloupnost čísel se zajímavou vlastností
Je dáno přirozené číslo $n$ a hledá se $2n+1$ po sobě jdoucích přirozených čísel s touto vlastností: součet druhých mocnin prvních $n+1$ čísel se rovná součtu druhých mocnin posledních $n$ čísel. Vypadá to složité? Ve skutečnosti k tomu nepotřebujete znát o moc víc než řešení kvadratické rovnice. Kdyby se někomu úloha s obecným $n$ zdála příliš složitá, může to zkusit pro konkrétní $n$, např. pro $n=10$, ale lepší je využít krásu a sílu matematiky a provést to najednou pro každé přirozené číslo $n$.Úloha byla zařazena do školní části 33. ročníku Matematické olympiády v kategorii A pro studenty středních škol.
Řešení
Mnohoúhelník složený z trojúhelníků
Rozdělit jakýkoli konvexní mnohoúhelník na trojúhelníky je velmi jednoduché. Budeme-li však chtít, aby všechny takto vzniklé trojúhelníky byly podobné, u každého kovexního mnohoúhelníku se nám to zřejmě nepodaří. Trochu to tedy zjednodušíme. Zkuste najít největší přirozené číslo $n$ takové, že existuje konvexní $n$-úhelník, který lze rozložit na pravoúhlé trojúhelníky s dvěma vnitřními úhly velikostí $30^\circ$ a $60^\circ$. (Trojúhelníky samozřejmě nemusejí být stejně velké.)Úloha byla zařazena do prvního kola 33. ročníku Matematické olympiády v kategorii A pro studenty středních škol.
Řešení
Jednoduchá hra pro samotáře
Na stole je pět žetonů. Tři jsou červené, dva modré a jsou srovnány v řadě vedle sebe tak, že se jejich barvy střídají: červený, modrý, červený, modrý, červený. Tah ve hře spočívá v tom, že některou dvojici sousedících žetonů přemístíme na jiné místo tak, že se přitom jejich vzájemná pozice nezmění (zůstanou těsně vedle sebe a ten, který byl vlevo, zůstane vlevo). Cílem hry je dosáhnout toho, aby po několika takových tazích bylo všech pět žetonů opět v řadě vedle sebe, přičemž nejprve jsou tři červené a za nimi dva modré. Na obrázku je výchozí a cílový stav: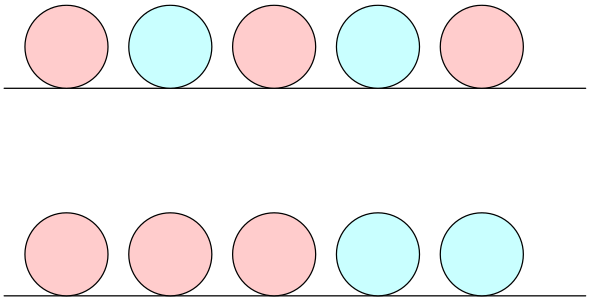
Řešení
Kde je princezna?
Honza se zase jednou přišel ucházet o princeznu. Princezně se Honza líbí, ale král chce zjistit, jestli to není hloupý Honza. Přivede Honzu před troje dveře do tří komnat a řekne mu, že musí přijít na to, ve které komnatě je princezna. Na prvních dveřích je nápis "princezna není ve druhé komnatě", na druhých je nápis "princezna není v této komnatě" a na třetích dveřích je nápis "princezna je v této komnatě". Král Honzoví vysvětlí, že aspoň jeden z nápisů je pravdivý a aspoň jeden z nápisů je nepravdivý. Za kterými dveřmi je princezna?Řešení
Koule a krychle
Je dána krychle $ABCDEFGH$ o hraně délky $a$. Určete střed a délku poloměru $r$ kulové plochy, která protíná stěnu $BCG$ v kružnici $k$ vepsané čtverci $BCGF$ a prochází středem $P$ strany $AB$.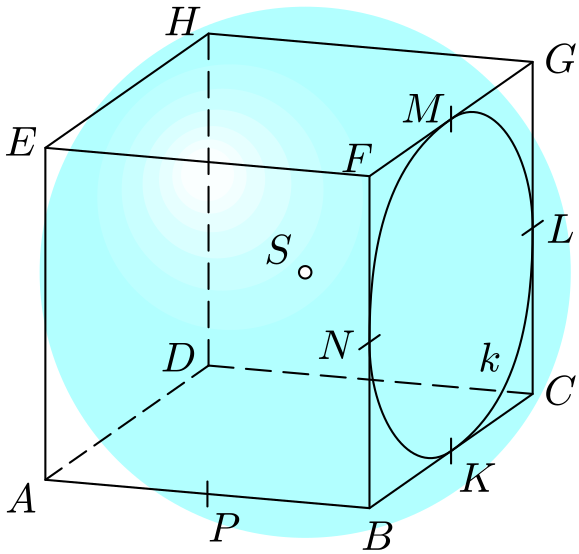
Řešení
Je to druhá mocnina?
Vytvoříme číslo $n$ tak, že postupně za sebou napíšeme prvních $400$ přirozených čísel: $n=12345\dots398399400$. Zjistěte, zda $n$ je druhou mocninou nějakého přirozeného čísla.Řešení
Která autíčka jsou nejrychlejší?
V kroužku modelářů mají závodní dráhu, na které může současně závodit 5 autíček. V depu kroužku je 25 autíček. Každé z nichž jezdí jinou, vždy však stejnou rychlostí. Kolik závodů musejí modeláři uspořádat, aby zjistili, která tři autíčka jsou nejrychlejší?Řešení
Čtyřúhelník v kruhu
Konvexní čtyřúhelník, kterému lze opsat kružnici a jehož úhlopříčky jsou na sebe kolmé, má zajímavou vlastnost: Součet druhých mocnin délek jeho dvou protějších stran se rovná druhé mocnině průměru kružnice opsané.
Tato úloha byla zařazena do druhého kola 33. ročníku Matematické olympiády v kategorii B pro studenty středních škol.
Řešení
Šest čísel
Čtyři přímky na obrázku se protínají v šesti průsečících.
Řešení
Která ze sedmadvaceti mincí je falešná?
Máme dvojramenné váhy a 27 na pohled stejných mincí. Všechny až na jednu mají stejnou hmotnost, jedna je nepatrně lehčí. Úkolem je trojím vážením najít tuto falešnou minci.Řešení
Je každý trojúhelník rovnoramenný?
Péťa, kterého baví objevovat matematiku, se zase jednou ukvapil (viz úlohu Kružnice se dvěma středy) a přišel s důkazem, že každý trojúhelník je rovnoramenný. Nakreslil následující obrázek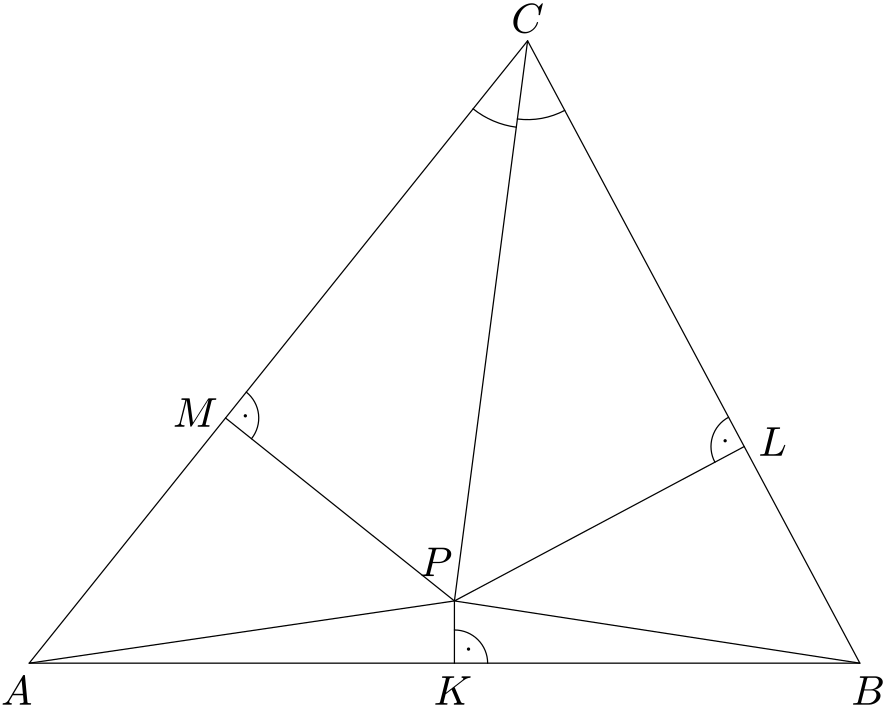
Řešení
Archiv úloh z předchozích týdnů
Ještě jeden trik s čísly
Zvolte si libovolné trojciferné číslo a zapište ho čtyřikrát za sebou. Vzniklé dvanáctimístné číslo je dělitelné čtyřcifernými čísly $1001$, $1111$, $1313$, $7777$, $9191$ a $9901$. Umíte to vysvětlit?Řešení
Číslování v trojúhelníkové síti
Je dán trojúhelník, jehož vrcholy jsou označeny čísly 1, 2, 3. Tento základní trojúhelník je rozdělen na konečný počet menších trojúhelníků tak, že každé dva z nich mají společný nejvýše jeden vrchol nebo jednu celou stranu. Každý z vrcholů menších trojúhelníků je označen jedním z čísel 1, 2, 3 tak, že na žádné straně základního trojúhelníku se nevyskytuje číslo jeho protějšího (tj. žádný z vrcholů menších trojúhelníků ležících na straně 12 základního trojúhelníku není označen číslem 3 atd.). Dokažte, že alespoň jeden z menších trojúhelníků má vrcholy označeny třemi různými čísly 1, 2, 3.
Řešení
Středy tří kružnic
Tři kružnice $k_1$, $k_2$, $k_3$ se středy v bodech $S_1$, $S_2$, $S_3$ se vzájemně dotýkají tak, jak je znázorněno na obrázku.
Řešení
Která z devíti mincí je falešná?
Máme dvojramenné váhy a devět na pohled stejných mincí. Osm z nich má stejnou hmotnost, devátá mince je falešná, je nepatrně lehčí. Úkolem je pouhým dvojím vážením určit, která mince je falešná.Řešení
Schůzka
Petr s Lucií si domluvili schůzku. Vědí, že oba jsou nedochvilní a současně netrpěliví, a proto se dohodli, že se sejdou v rozmezí od 18:00 do 19:00 hodin, ale nikdo nebude na druhého čekat déle než 10 minut. Jak velká je pravděpodobnost, že se opravdu setkají, pokud se oba dostaví na schůzku v daném rozmezí 18:00–19:00 hodin?Řešení
Pythagorova věta
Pythagorova věta je matematické tvrzení, které zná (nebo o něm alespoň slyšel) snad každý, kdo prošel základním vzděláním: obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Existuje celá řada důkazů, viz např. tento obrázek:
Výše uvedená formulace Pythagorovy věty však neříká nic o tom, že tato věta platí pouze pro pravoúhlé trojúhelníky. Umíte to dokázat?
Řešení
Hledá se prvočíslo
Pro které prvočíslo $p$ je $2p+1$ třetí mocninou nějakého přirozeného čísla?Řešení
Poutník
Poutník vyšel v 6:00 z hostince při úpatí hory a po stezce vinoucí se kolem hory vzhůru stoupal celý den na vrchol. Strávil noc v bivaku, ráno se pokochal pohledem na vycházející slunce, v 6:00 vyrazil stejnou cestou zpět a vrátil se do hostince na večeři. V obou směrech samozřejmě postupoval různou a nepravidelnou rychostí, zastavoval se na odpočinek. Přesto je jisté, že na cestě existuje místo, ve kterém se poutník nacházel v obou dnech ve stejném čase. Umíte to vysvětlit?Řešení
Kružnice se dvěma středy
Péťu matematika baví, ale občas se ukvapí. Onehdá se přihlásil s objevem, že kružnice může mít dva různé středy. Nakreslil následující obrázek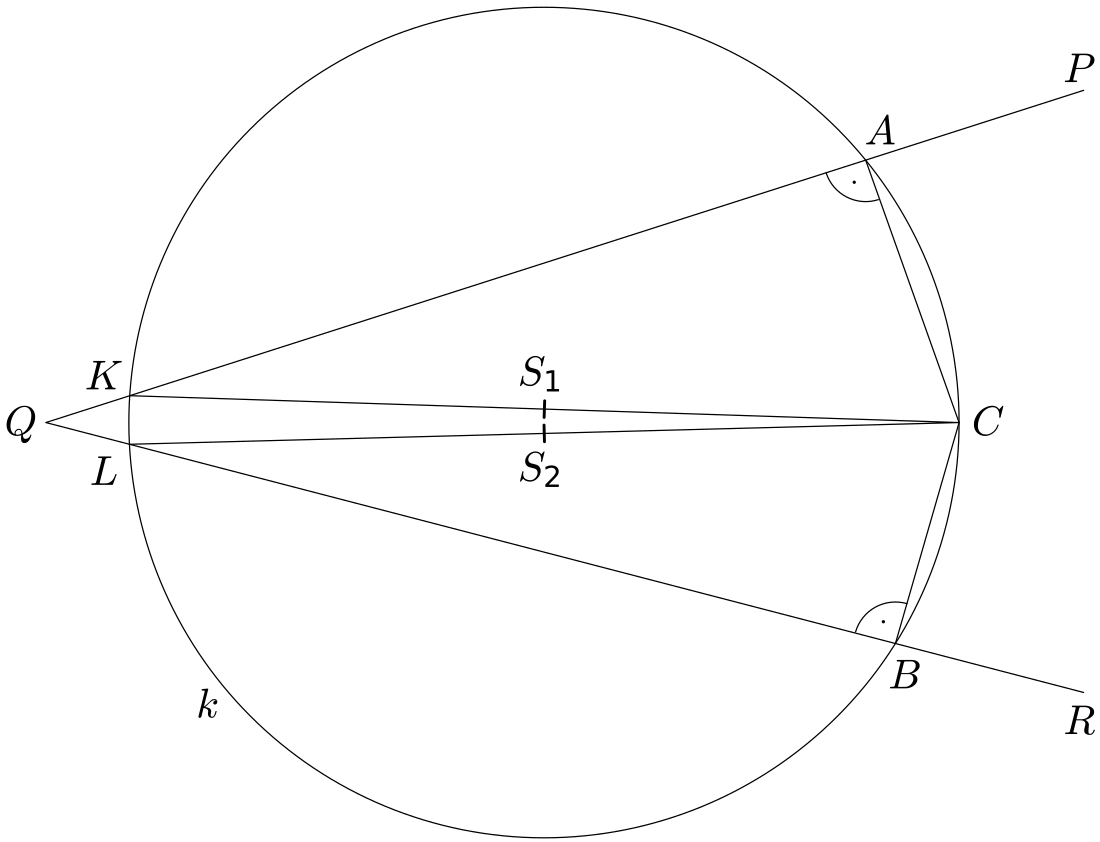
Řešení
Co je výhodnější?
Pan Novák vyjednává se zaměstnavatelem o své mzdě. Dostal dvě nabídky: mzda bude zvyšována buď po každém roce tak, že celková mzda vyplacená za celý rok vzroste o 10 000 Kč, nebo po každém pololetí tak, že celková mzda vyplacená za příslušné pololetí vzroste o 2 500 Kč. Kterou nabídku by si měl vybrat?Řešení
Podivný rozsudek
V pondělí odpoledne skončil proces s nebezpečným zločincem vynesením rozsudku: "Obžalovaný se odsuzuje k trestu smrti oběšením. Rozsudek musí být vykonán v pravé poledne některého dne v tomto týdnu za podmínky, že o tom, kterého dne bude rozsudek vykonán, obžalovaný nesmí vědět dříve než v ten samý den ráno." Obžalovaný, který byl připraven na nejhorší, po vynesení rozsudku neskrýval svou spokojenost. Přijdete na to proč?Řešení
Kam postavit trafiku?
Tři ulice se protínají po dvou tak, že tvoří náměstí tvaru rovnostranného trojúhelníku. Trafikant by chtěl postavit svou trafiku na náměstí a domnívá se, že nejlepší poloha bude taková, aby součet vzdáleností trafiky od všech tří ulic byl nejmenší. Kam má svou trafiku umístit?
Řešení
Jednoduchá hra
Hrací plán tvoří pravidelný desetiúhelník s poli ve vrcholech očíslovanými od 0 do 9 ve směru pohybu hodinových ručiček. Na začátku hry se na pole 0 položí kámen.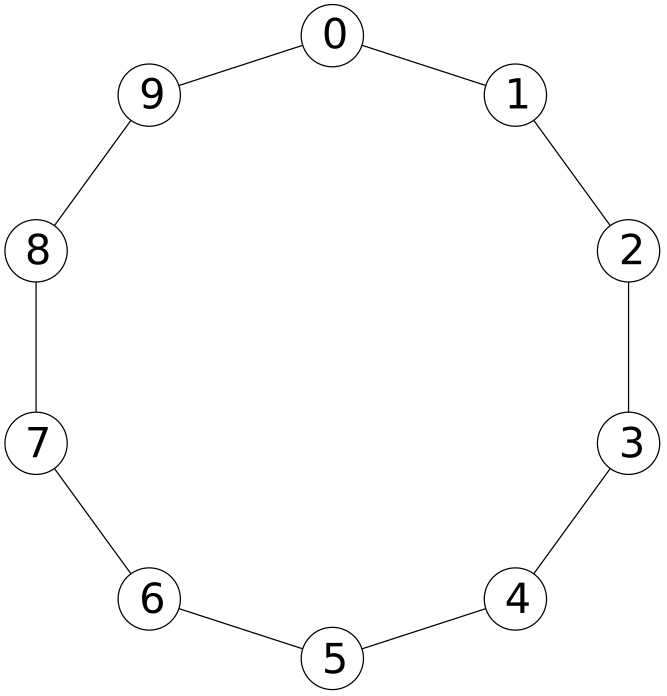
Řešení
Patnáct časopisů na stole
Matematik zašel s přítelkyní do kavárny. Posadili se k jedinému volnému stolku, který však byl zcela pokrytý časopisy. Přítelkyně svého partnera již dobře znala, a tak ji nepřekvapilo, když poznamenal: "Těch časopisů je patnáct. Sedm z nich bychom mohli odstranit a zbývajících osm by stále ještě pokrývalo nejméně osm patnáctin desky stolku." Měl pravdu?Řešení
Dvě kružnice vepsané do lichoběžníku
Do lichoběžníku $ABCD$, který má tu vlastnost, že součet délek základen $a$, $c$ je větší než součet délek ramen $b$, $d$, jsou vepsány dvě kružnice $k_1$, $k_2$.
Řešení
Třetí mocnina končící na 2021
Která přirozená čísla mají tu vlastnost, že jejich třetí mocnina končí na 2021?Řešení
Sedmnáctiúhelník a tři barvy
V pravidelném sedmnáctiúhelníku je každá dvojice jeho vrcholů spojena úsečkou. Každá úsečka má modrou, červenou, nebo zelenou barvu. Existuje trojice vrcholů, které jsou spojeny úsečkami stejné barvy?Řešení
Čtyři kružnice v trojúhelníku
Je dán obecný trojúhelník $ABC$. K jemu vepsané kružnici jsou vedeny tři tečny rovnoběžné se stranami trojúhelníku. Tečny v trojúhelníku vytínají tři menší trojúhelníky, do nichž jsou opět vepsány kružnice.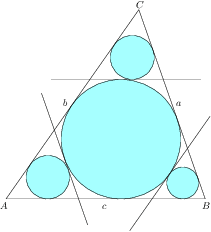
Řešení
Podivní příbuzní
Navštívili nás dva příbuzní, dospělý s dítětem. To dítě bylo synem dospělého, ale dospělý nebyl jeho otcem. Jak je to možné?Řešení
Další kouzla s čísly
Zvolte si libovolné trojciferné číslo a zapište ho dvakrát za sebou. Ověřte, že vzniklé šestimístné číslo je dělitelné jedenácti. Pak zkuste totéž s dvojciferným, čtyřciferným, pěticiferným, šesticiferným číslem. Která z výsledných čtyřciferných, osmiciferných, deseticiferných, dvanácticiferných čísel budou dělitelná jedenácti? Je v tom náhoda nebo nějaká zákonitost?Řešení
Krychle a koule
Uvnitř krychle o hraně délky $a$ určete všechny středy kulových ploch, které se dotýkají jejích tří sousedních stěn se společným vrcholem a tří sousedních hran, které v těchto stěnách neleží.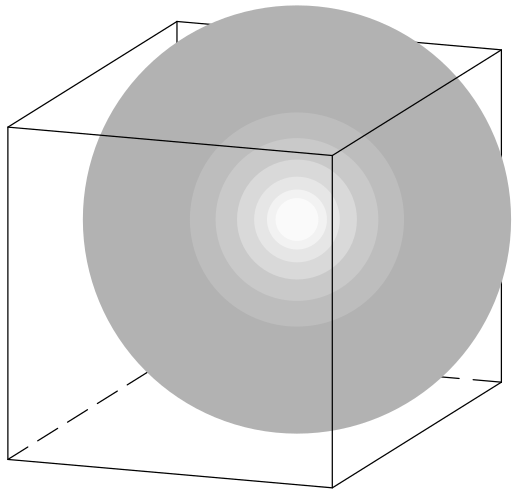
Řešení
Číslování dveří
Budova, ve které je sto dveří, se renovuje. Lakýrník má za úkol natřít všechny dveře a označit je všechny čísly od 1 do 100. Pro každou číslici má šablonu. Kolikrát použije šablonu, jejíž pomocí se maluje číslice 9?Řešení
Šikmá věž z cihel
Pro účel této úlohy si představme, že máme sadu cihel přesně stejné velikosti, hmotnosti a rovnoměrné hustoty. Položíme-li jednu cihlu na druhou, je jasné, jak daleko můžeme tu horní vysunout přes okraj té spodní, aniž by se překlopila a spadla: do poloviny. Těžiště horní cihly je pak přesně na hraně té spodní a nepřeklopí se.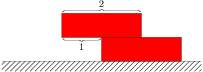
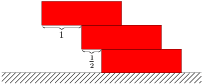
Řešení
Dva trojúhelníky
Je dán obecný trojúhelník $ABC$. Na jeho stranách zvolíme body $K$, $L$, $M$ tak, že $|AK|={1\over7}|AB|$, $|BL|={1\over7}|BC|$, $|CM|={1\over7}|CA|$. V jakém poměru jsou obsahy trojúhelníků $KLM$ a $ABC$?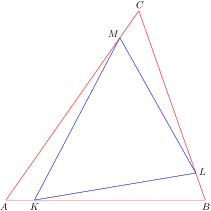
Řešení
Vyšetřování loupeže
Zlatník Crook oznámil, že mu někdo z obchodu ukradl náhrdelník s diamanty. Inspektor Smart na základě jeho výpovědi vyslechl tři podezřelé, kteří jako jediní v den krádeže zlatnictví navštívili, a zjistil následující skutečnosti:- (a) Pokud je pan Adams vinen, měl právě jednoho společníka.
- (b) Pokud je pan Brown nevinen, je nevinen i pan Campbell.
- (c) Pokud jsou vinni právě dva z podezřelých, pak jedním z nich je pan Adams.
- (d) Pokud je pan Campbell nevinen, je nevinen i pan Brown.
Řešení
Kouzelný čtverec
Ukážeme další kouzelnický trik, za kterým se skrývá jednoduchá matematika. Jardových slavil třicáté narozeniny. Protože o něm bylo známo, že se rád baví matematickými hádankami, jeden z hostů si vyžádal list papíru, nakreslil na něj následující čtvercovou mřížku a vyplnil ji čísly: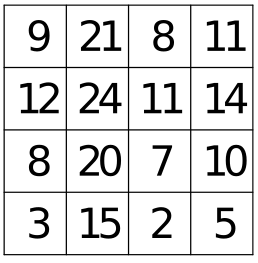
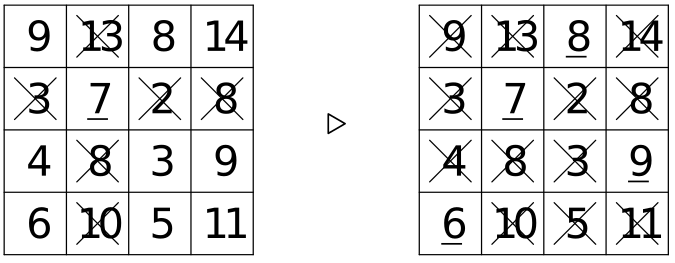
Řešení
Kružnice vepsaná do mnohoúhelníku
Je dána kružnice a jí opsaný konvexní mnohoúhelník. Uvnitř mnohoúhelníku je zvolen bod $X$. Úkolem je určit velikost poloměru kružnice pomocí vzdáleností bodu $X$ od jednotlivých stran mnohoúhelníku. Na obrázku je situace znázorněna pro případ sedmiúhelníku.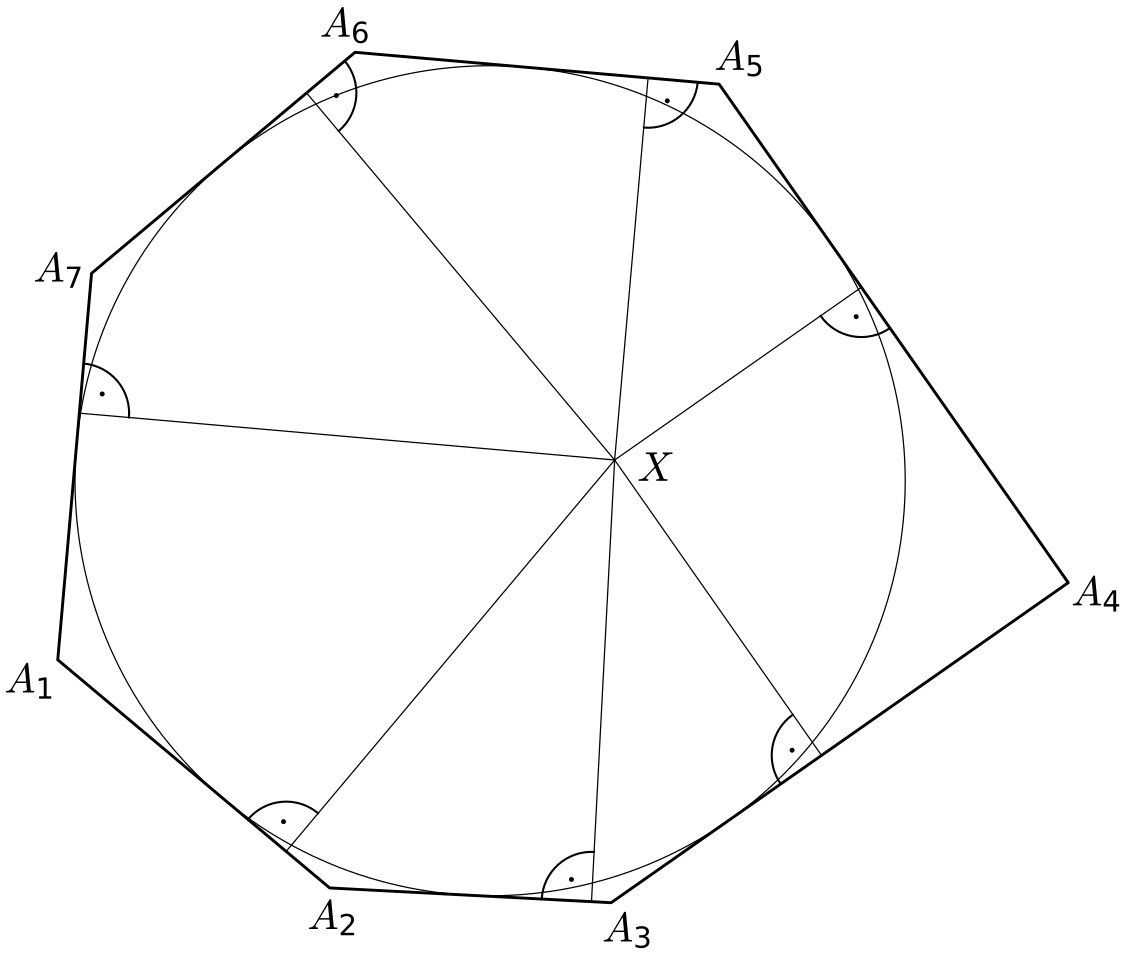
Řešení
Kde udělal Karel chybu?
Karel se v hodině matematiky přihlásil s tím, že v matematice objevil zásadní problém. Vyšlo mu, že $1=-1$. Předvedl následující postup: $$\eqalign{\sqrt{-1}&=\sqrt{-1}\cr \sqrt{1\over -1}&=\sqrt{-1\over1}\cr {\sqrt1\over\sqrt{-1}}&={\sqrt{-1}\over\sqrt1}\cr \sqrt1\cdot\sqrt1&=\sqrt{-1}\cdot\sqrt{-1}\cr 1&=-1}$$Řešení
Deset mincí
Máte deset mincí a víte, že aspoň jedna z nich je pravá. Některé z nich jsou však možná i falešné. Navíc víte, že všechny pravé mince váží stejně a všechny falešné mince váží stejně, jen nevíte, jestli jsou lehčí nebo težší než ty pravé. Máte také obyčejnou dvouramennou váhu. Vaším úkolem je co nejmenším počtem vážení zjistit, jestli jsou všechny mince pravé, nebo jestli mezi nimi je nějaká falešná.Snadno se to provede čtyřmi váženími: Porovnáme první dvě mince. Pokud jsou stejné, dáme obě mince na jednu misku a na druhou misku dáme další dvě. Jsou-li opět všechny stejné, dáme na jednu misku čtyři dosud zvážené mince a na druhou další čtyři mince. Jsou-li opět všechny stejné, porovnáme zbývající dvě mince se dvěma zváženými.
Existuje způsob, jak to provést jen třemi váženími?
Řešení
Paradoxní skládačka podruhé
V jedné z předchozích úloh jsme předvedli čtverec 8x8, který byl po rozřezání na čtyři na dva lichoběžníky a dva trojúhelníky složen do tvaru obdélníku 13x5, který má o jeden čtvereček větší obsah než původní čtverec. Nyní máme obrácenou situaci. Na obrázku vlevo je čtverec 13x13, který má obsah 139 čtverečků. Po rozřezání podle vyznačených čar jsou dva trojúhelníky a dva lichoběžníky na obrázku vpravo složeny do tvaru obdélníku 21x8 o obsahu 168 čtverečků. Tentokrát se nám jeden čtvereček ztratil.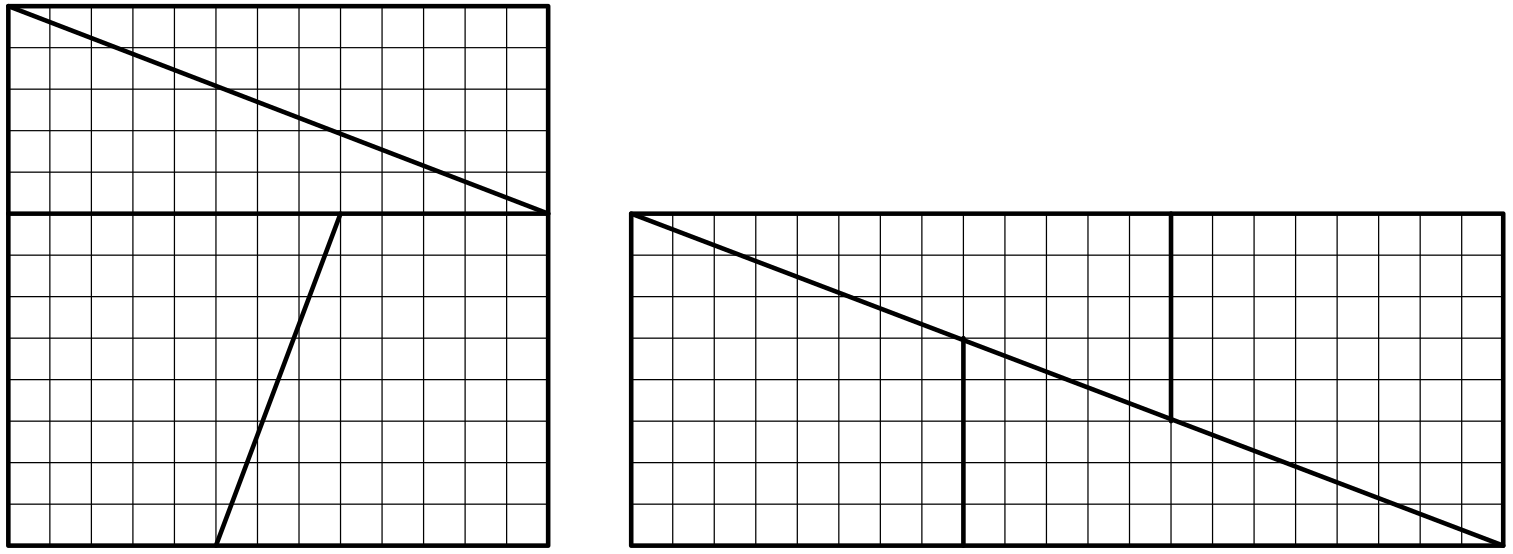
Řešení
Druhá odmocnina ze dvou není racionální číslo
Racionální číslo je reálné číslo, které lze vyjádřit jako podíl dvou celých čísel. Již ve starověku bylo známo, že odmocnina ze dvou není racionální číslo. Umíte to dokázat?Řešení
Počítání vlasů v Zapadlé Lhotě
V jedné z úloh jsme "počítali" vlasy Pražanů. V Zapadlé Lhotě je trochu složitější situace.- Žádní dva obyvatelé Zapadlé Lhoty nemají na hlavě přesně stejný počet vlasů.
- Počet obyvatel Zapadlé Lhoty je větší než počet vlasů na hlavě kteréhokoli z jejích obyvatel.
- Žádný z obyvatel Zapadlé Lhoty nemá na hlavě přesně $99$ vlasů.
Řešení
Paradoxní skládačka
Na obrázku vlevo je čtverec 8x8 s vyznačenými čarami. Když ho podle těchto čar rozřežeme na dva lichoběžníky a dva trojúhelníky a složíme podle obrázku vlevo, dostaneme obdélník 13x5. Zatímco původní čtverec měl obsah 64 čtverečků, obdélník má obsah 65 čtverečků.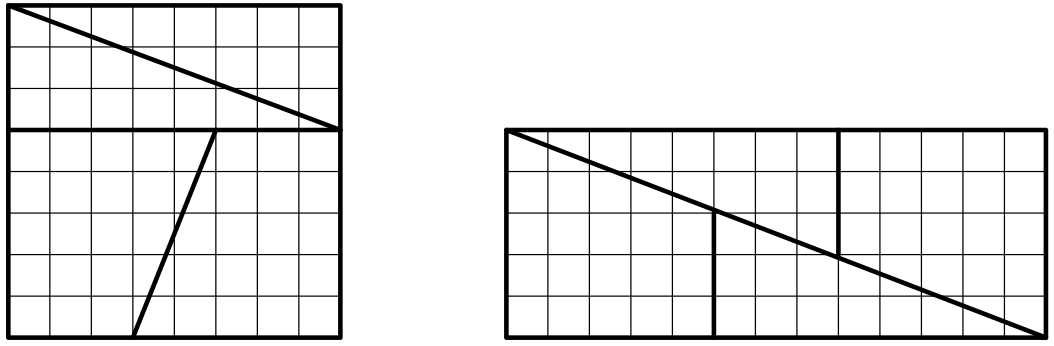
Řešení
Všechna čísla jsou si rovna?
Vezměme dvě různá čísla $a$, $b$ a jejich rozdíl označme $c$, $c=b-a$. Proveďme postupně následující úpravy: $$\eqalign{a&=b+c \quad /\cdot(a-b)\cr a^2-ab&=ab+ac-b^2-bc\cr a^2-ab-ac&=ab-b^2-bc\cr a(a-b-c)&=b(a-b-c)\quad /:(a-b-c)\cr a&=b} $$ Ouvej! Kde jsme udělali chybu?Řešení
Obsah mezikruží
Na obrázku je vybarveno mezikruží vytvořené dvěma soustřednými kružnicemi. Červeně vyznačená úsečka je nejdelší tětivou větší kružnice dotýkající se menší kružnice (je to samozřejmě jedna z nekonečně tětiv těchto vlastností). Tětiva má délku $t$.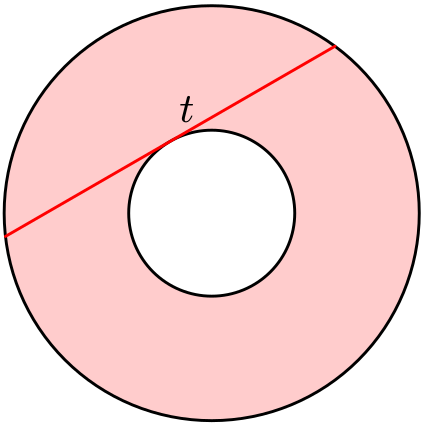
Řešení
Dvě mince
Mám dvě mince, jejichž ceková hodnota je 30 Kč, ačkoli jedna z nich není desetikoruna. Jak je to možné?Řešení
Dva běžci
Dva žáci stojí na opačných koncích běžecké dráhy na školním hřišti. Na povel současně vyběhnou proti sobě. Každý z nich běží stálou rychlostí. Když se poprvé minou, pomalejší z nich uběhl 35 m. Po doběhu na konec dráhy se každý otočí a běží zpět. Když se setkají podruhé, ten pomalejší uběhl 15 m od otočky. Jak dlouhá je běžecká dráha?Řešení
Čtyři roboti
Členové kroužku kybernetiky zkonstruovali čtyři robotická vozítka naprogramovaná tak, že se všechna pohybují stejnou stálou rychostí a v každém okamžiku se robot A pohybuje přesně ve směru robota B, robot B se pohybuje přesně ve směru robota C, robot C přesně ve směru robota D a robot D přesně ve směru robota A. Umístili roboty na podlahu do vrcholů čtverce v pořadí A, B, C, D ve směru pohybu hodinových ručiček a najednou je spustili. Je zřejmé, že každý z robotů se pohybuje po spirálové dráze směrem do středu čtverce. Jak dlouhou cestu každý z nich urazí do setkání upostřed čtverce? (Pro jednoduchost zanedbáváme velikost robotů, takže se roboti setkají přesně uprostřed čtverce.)Řešení
Za kterými dveřmi je princezna?
Honza se přišel ucházet o princeznu. Krále ta troufalost překvapí, ale princezně se Honza líbí a na její prosbu mu dá šanci. Přivede ho před troje dveře do tří komnat a řekne mu, že v jedné komnatě je princezna, v jedné je žalářník, jedna komnata je prázdná. Honza dostane princeznu, když ukáže na dveře do komnaty s princeznou. Když ukáže na dveře do komnaty s žalářníkem, ten ho odvede do šatlavy. Když ukáže na dveře prázdné komnaty, princeznu nedostane, ale nic se mu nestane. Na prvních dveřích je nápis "za těmito dveřmí je princezna", na druhých je nápis "za těmito dveřmí princezna není" a na třetích dveřích je nápis "princezna není za prvními dveřmi". Král Honzoví vysvětlí, že nejvýše jeden z nápisů je pravdivý. Za kterými dveřmi je princezna?Řešení
$a=0$?
Eva si procvičovala úpravy algebraických výrazů a vyšlo jí, že každé reálné číslo je rovno nule: $$\eqalign{a&=b\quad /\cdot a\cr a^2&=ab\cr a^2-ab&=0\cr a(a-b)&=0\quad /:(a-b)\cr a&=0} $$ To jistě nemůže být pravda. Co udělala špatně?Řešení
Délka úhlopříčky
Do čtvrtkruhu o poloměru $2a$ je vepsán obdélník $ABCD$ vyznačený modře na obrázku: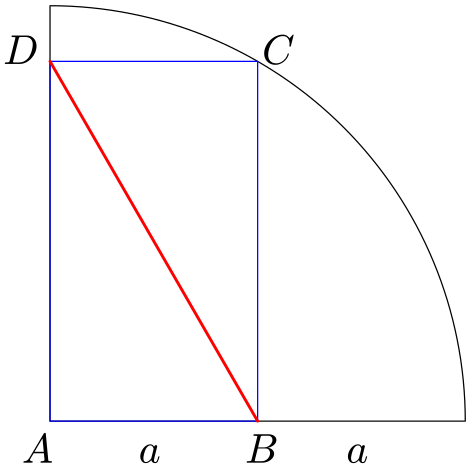
Velká rodinná oslava
Rodina se sešla na oslavě narozenin babičky, která již bohužel nevidí, ale zachovala si své schopnosti vynikající počtářky. Sešlost se skládá z babičky a dědečka, dvou otců, dvou matek, čtyř dětí, tří vnoučat, bratra, dvou sester, dvou synů, dvou dcer, tchána, tchyně a snachy. Na babiččinu otázku, kolik lidí na oslavu přišlo, vnučka Anička, která zdědila nadání po babičce, odpoví šibalsky: "Babičko, pokud bys vzala libovolné dvojciferné číslo a třikrát ho zapsala za sebou, výsledné šestimístné číslo bude zcela jistě dělitelné počtem přítomných osob."Jaký je nejmenší počet účastníků oslavy a proč je každé šestimístné číslo sestavené výše uvedeným způsobem dělitelné tímto nejmenším počtem?
Řešení
Pokrývání šachovnice
Vlevo na obrázku je šachovnice, ze které bylo vyříznuto levé horní a pravé dolní bílé pole. Vedle šachovnice je znázorněna kostka domina, která přesně pokrývá dvě sousední pole šachovnice. Lze takovými kostkami domina pokrýt celou desku bez dvou polí znázorněnou vlevo tak, aby se kostky nepřekrývaly? A co když místo dvou rohových polí vyřízneme dvě pole uprostřed znázorněná na pravé šachovnici modře?

Řešení
Jak rozřezat krychli?
Truhlář dostal za úkol rozřezat pilou dřevěnou krychli na 9 stejně velkých krychliček. To je snadný úkol: stačí na hraně krychle vyznačit její třetiny a vést tudy řezy kolmé k hraně a totéž pak zopakovat u dvou sousedních hran. Stačí tedy celkem 6 řezů. Truhlář však raději přemýšlel, než by se zbytečně namáhal a zamyslel se nad tím, jestli neexistuje šikovný způsob, jak krychli rozřezat menším počtem řezů. Umíte mu poradit?Řešení
Halloween a Vánoce
Tahle úloha je spíš trochu silvestrovská. Zlí jazykové tvrdí, že si angličtí matematici pletou Halloween a Vánoce. Víte proč?Řešení
Kouzla s čísly jinak
Už jsme tu měli jednoho kouzelníka udivujícího kouzly s čísly. Tentokrát kouzelník vyvolal diváka a požádal ho, aby hodil třemi obyčejnými hracími kostkami, ale aby mu neukazoval, co padlo. Potom mu řekl: "První číslo vynásobte dvěma a přičtěte k němu pět, výsledek vynásobte pěti a přičtěte k tomu číslo na druhé kostce. Výsledek vynásobte deseti a přičtěte k tomu číslo na třetí kostce. Kolik vám vyšlo?" Když divák řekl 817, kouzelník ho pokáral, ať si to přepočítá, že určitě udělal chybu. Divák se omluvil, že se skutečně spletl, že správný výsledek je 814. Kouzelník se zahleděl do dálky, cosi zamumlal a řeknl: "Tak to je jasné. Na první kostce padlo 5, na druhé 6 a na třetí 4." Jak to dokázal? A jak přišel na to, že se divák poprvé spletl?Řešení
Tři hlavolamy se zápalkami
Máte dobrou představivost? V obrazci vlevo je vaším úkolem odebrat nejmenší počet zápalek tak, aby zbylé zápalky tvořily čtyři stejné rovnostranné trojúhelníky. V obrazci uprostřed je vaším úkolem přemístit co nejmennší počet zápalek tak, aby ryba plula opačným směrem. Jaký nejmenší počet zápalek je třeba přemístit ve třetím obrazci, aby oliva byla mimo sklenici?
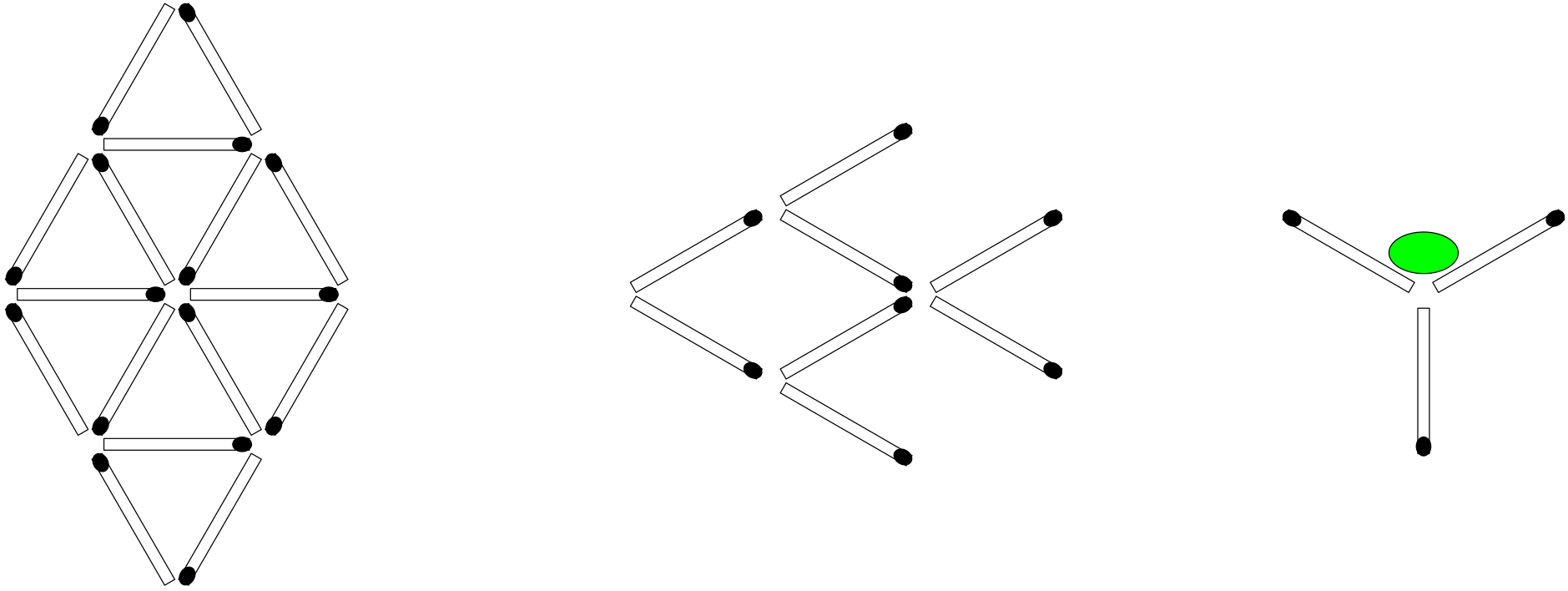
Řešení
Změna pořadí číslic
Existuje celé kladné číslo, jehož šestinásobek je vyjádřen stejnými číslicemi uspořádanými v opačném pořadí?Úloha je překvapivě snadná, přestože pochází z Matematické olympiády v Německu v roce 1961, kde byla zařazena do třetího kola ze čtyř pro kategorii žáků 11. tříd.
Řešení
Ponožky v šuplíku
V šuplíku je pět párů černých a pět párů bílých ponožek. Kolik ponožek musím vytáhnout poslepu z šuplíku, abych měl jistotu, že budu mít aspoň jeden pár stejné barvy?Tak to je známá a hodně snadná úloha. Trochu to zkomplikujeme. V šuplíku mám určitý počet černých a stejný počet bílých ponožek. Kolik jich v šuplíku je, když vím, že nejmenší počet ponožek, které musím vytáhnout, abych s jistotou měl alespoň jeden pár stejné barvy, je stejný jako nejmenší počet ponožek, které musím vytáhnout, abych s jistotou měl alespoň dvě ponožky různé barvy?
Řešení
Jak udělat čtvercovou desku?
Truhláři ve skladu zbyl kus dřevěné desky tohoto tvaru:
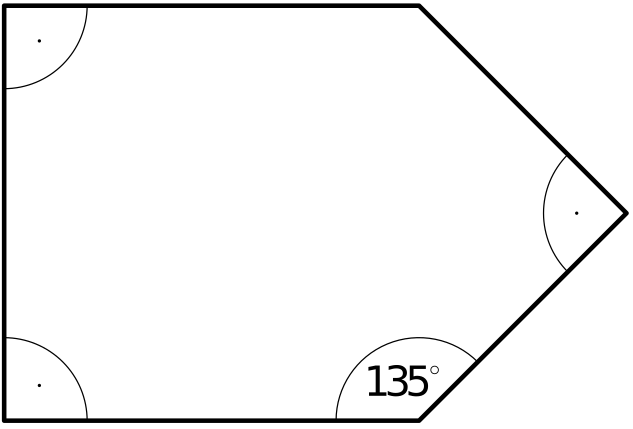
Řešení
Je na ostrově trosečník?
Loď ztroskotala v oblasti souostroví, o jehož obyvatelích je známo, že každý z nich buď vždy mluví pravdu nebo vždy lže. Záchranná výprava hledající trosečníky připluje k ostrovu a ptá se domorodce, jestli je na ostrově nějaký trosečník. Domorodec odpoví: "Je tu trosečník, právě když jsem pravdomluvný." Je ten domorodec pravdomluvný nebo lhář? Lze z jeho odpovědi usoudit, zda je na ostrově trosečník?Řešení
Utajené číslo
Mezi úlohami pro řešitele Matematické olympiády v Německu v roce 2010 se v oblastním kole objevila následující úloha. (Šlo o druhé kolo ze čtyř, obtížnost úloh byla ještě poměrně nízká.) Čtyři kamarádi, Alena, Bára, Cyril a David se dohodli na určitém čísle, zapsali ho na papír. Každý z nich o tom čísle vyslovil dva výroky, z nichž vždy jeden je pravdivý a druhý nepravdivý. Výroky, označené počátečními písmeny jejich jmen, zněly takto:
A1: "Číslo je trojciferné."
A2: "Součin všech jeho číslic je $23$."
B1: "Číslo je dělitelné $37$."
B2: "V zápisu čísla se vyskytují tři stejné číslice."
C1: "Číslo je dělitelné $11$."
C2: "Na posledním místě je číslice $0$."
D1: "Ciferný součet je větší než $10$."
D2: "Číslice na pozici stovek není největší ani nejmenší ze všech číslic."
Řešení
Kužel a koule ve válci
Do rotačního válce o poloměru $R$ je vložen kužel, který má s válcem společnou podstavu a jehož vrchol splývá se středem horní podstavy válce. Uvnitř válce je umístěno šest stejných koulí takovým způsobem, že se každá dotýká sousedních dvou koulí, pláště kužele, pláště a horní podstavy válce. Vypočtěte poloměr $\rho$ největší koule vložené do kužele.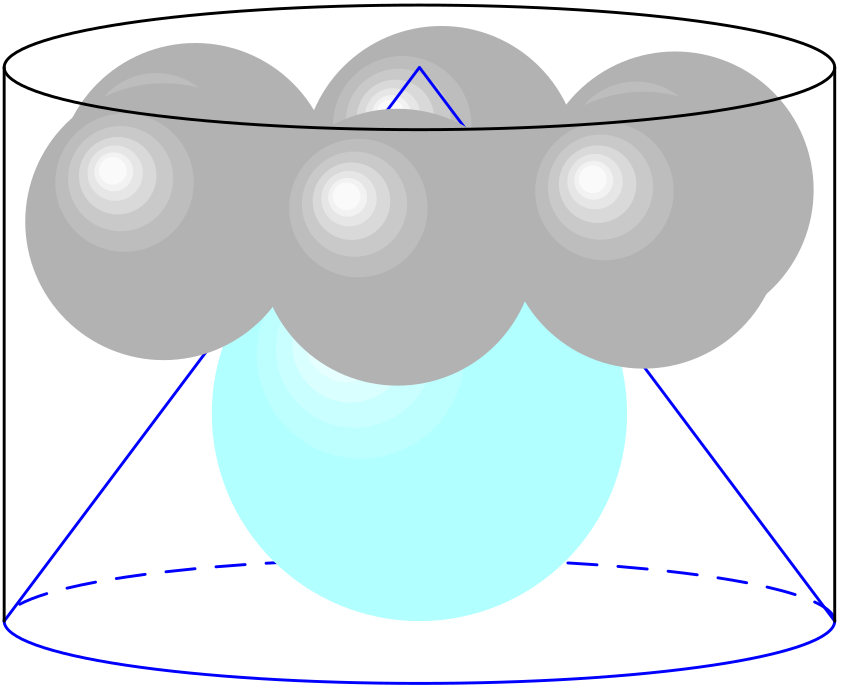
Řešení
Kouzla s čísly
Někteří kouzelníci rádi udivují diváky svými "nadpřirozenými" schopnostmi v oblasti čísel. Takový kouzelník třeba vyvolá diváka a požádá ho, aby si na papír poznamenal libovolné dvojciferné číslo a aby ho zapsal čtyřikrát za sebou a vytvořil tak osmiciferné číslo. Pak ho požádá třeba o jeho datum narození, směrovací číslo nebo cokoli jiného, "zamyslí se" a pak oznámí, že výsledné osmimístné číslo je dělitelné číslem $73$. Jak to dokázal?Řešení
Složitější hra s čepičkami
Tato hra je náročnější. Skupině lidí vysvětlíme pravidla a dáme jim čas na domluvu o vhodné strategii. Pravidla jsou následující: Účastníci se seřadí do zástupu podle velikosti tak, že na začátku stojí nejmenší, na konci největší. Každý se smí dívat jen dopředu na ty menší, které má před sebou. Každému účastníku pak dáme na hlavu černou nebo bílou čepičku tak, aby neviděl, jakou má barvu. Na dané znamení jeden po druhém postupně od největšího po nejmenšího řekne buď "černá", nebo "bílá", nic jiného. Úkolem je dosáhnout toho, že se nejvýše jeden hráč zmýlí při určení barvy čepičky na své hlavě. Jakou strategii mají hráči zvolit?Řešení
Úhly v krychli
Na stěnách krychle na obrázku jsou červeně vyznačeny dvě úsečky spojující středy hran. Jaký úhel svírají?
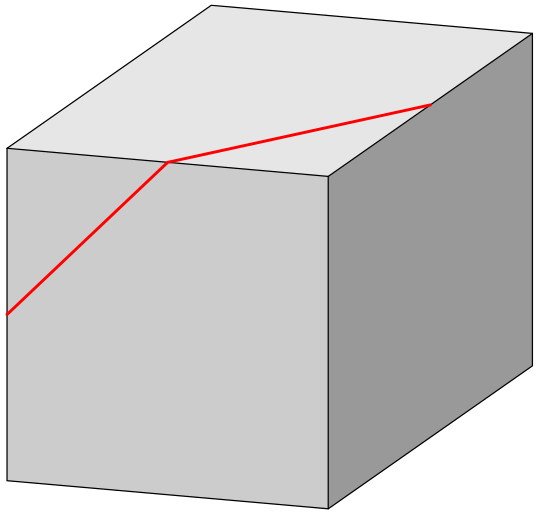
Řešení
Falešné mince podruhé a složitěji
Před několika týdny jsme tu měli klasickou úlohu, jak jedním vážením zjistit, ve kterém pytli jsou ošizené, o $1$ gram lehčí mince. Král se dozvěděl, že se ho mincmistr pokusil ošidit a vyrobil několik pytlů mincí, které váží o $1$ gram méně než předepsaných $10$ gramů. Nechal z mincovny přinést $6$ pytlů s vyrobenými mincemi, předvolal si mincmistra a řekl mu, že když nedokáže jedním vážením zjistit, ve kterých pytlech jsou ty lehčí mince, bude popraven. Jak si mincmistr zachrání život? Úloha je složitější v tom, že pytlů s ošizenými mincemi může být víc.Řešení
Komu věřit?
Opět jsme na logiky oblíbeném ostrově, kde každý domorodec je buď pravdomluvný nebo je lhář. Poutník má v cestě rozbouřenou řeku a chce zjistit, kterým směrem je nejbližší most. Na druhém břehu stojí tři domorodci. Poutník potřebuje zjistit, kdo je pravdomluvný. Zavolá na prvního: "Jsi pravdomluvný?" Odpověď se však ztratí v hukotu vody. Zavolá na druhého domorodce: "Odpověď nebyla slyšet. Co řekl ten člověk?" Druhý odpoví: "Jsem pravdomluvný." Poutník ještě zavolá na třetího: "Jsi pravdomluvný nebo lhář? A jací jsou ti druzí dva?" Otázaný odpoví: "Jsem pravdomluvný. Ti další dva jsou lháři." Koho se má poutník zeptat na cestu k mostu?Řešení
Koule v krychli
Krychli o hraně délky $a$ je vepsána koule o poloměru ${a\over2}$ se středem ve středu krychle. Do prostoru mezi koulí a stěnami krychle je vložena menší koule, která se dotýká větší koule a tří stěn krychle.
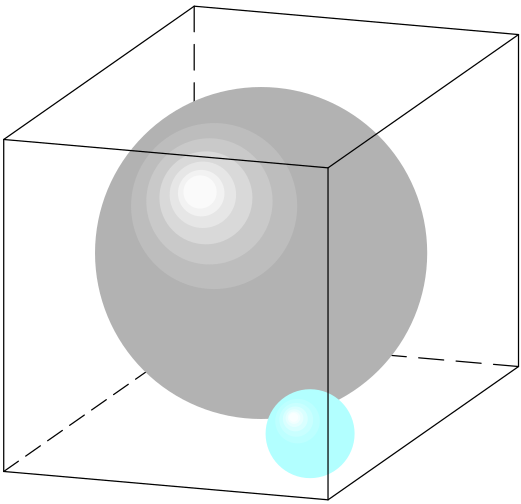
Řešení
Devíticiferná čísla dělitelná 45
Kolik existuje devíticiferných čísel dělitelných $45$ a sestavených z číslic $1,2,3,\dots,9$ tak, že každá z těchto číslic se v jejich vyjádření vyskytuje přesně jednou?Řešení
Kde je princezna?
Jak to v pohádkách bývá, Honza chce získat princeznu, musí však prokázat, že není žádný hloupý Honza. Král ho přivede do komnaty se dvěma závěsy. Má uhodnout, za kterým z nich je princezna ukryta. V komnatě stojí dva sluhové, kteří vědí, kde princezna je. Honza však smí položit jen jednomu z nich jedinou otázku. Král Honzovi řekne, že jeden sluha má příkaz odpovídat pravdivě, druhý nepravdivě. Jak to Honza udělá, aby princeznu získal?Řešení
Arbelos
V úloze o Archimedových kruhových dvojčatech jsme již uvedli, že vybarvenému obrazci na obrázku se říká arbelos.
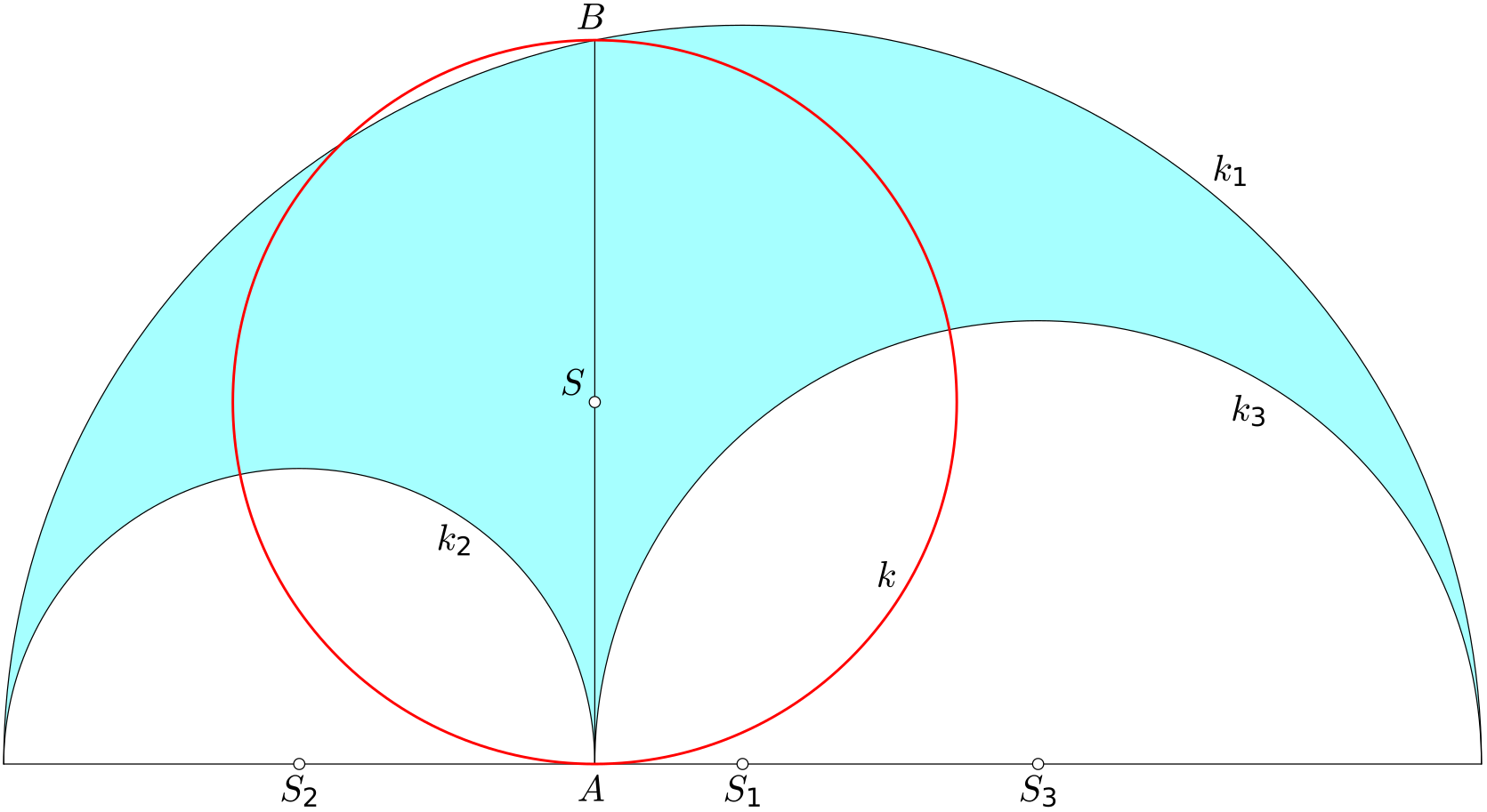
Arbelos má jako geometrický útvar řadu pozoruhodných vlastností a souvislostí. Umíte ukázat, že plošný obsah arbelu je roven obsahu kruhu ohraničeného červenou kružnicí na obrázku?
Řešení
První a poslední číslice
Určete prvních devět a posledních devět číslic podílu $3\underbrace{000000\dots00000}_{{\rm 99\ nul}}7:37$ a zbytek dělení.Řešení
Lháři a pravdomluvní u kulatého stolu
U kulatého stolu se sešla skupina lidí, z nichž někteří jsou pravdomluvní a někteří jsou lháři. Každý z nich tvrdí o svých dvou sousedech, že jsou lháři. Jeden z nich prohlásí, že kolem stolu sedí celkem jedenáct lidí. Druhý mu odporuje a řekne: "Lžete! Je nás deset." Kolik lidí tvoří tuto společnost? Kolik je mezi nimi lhářů?Řešení
Čtvrkruh a polokružnice
Je dán čtvrtkruh a do něj jsou vepsány dvě polokružnice, jejichž průměry splývají s poloměry daného čtvrtkruhu:
Autorem této úlohy je japonský tvůrce matematických hlavolamů Kobon Fujimura.
Řešení
Kolik zbylo na sestru?
Dva bratři se rozhodli prodat svou sbírku plastových autiček. Za celou sbírku dostali tolik peněz, že na jedno autičko v průměru připadlo tolik korun, jako byl počet všech autíček ve sbírce. Dohodli se na následujícím dělení zisku. Starší bratr si vezme 10 Kč, pak si mladší bratr vezme 10 Kč, pak si opět starší vezme 10 Kč, atd. Případný zbytek (menší než 10 Kč) věnují své sestře. Dopadlo to tak, že poslední desetikorunu si vzal starší bratr. Kolik korun dostala sestra?Řešení
Otázka, na kterou ani Děd Vševěd neumí odpovědět
Děd Vševěd přece ví vše, a tedy umí odpovědět na každou otázku. Opravdu? Umíte zformulovat otázku, na kterou ani Děd Vševěd nenajde odpověď?Řešení
Úhly v krychli
Na stěnách krychle na obrázku jsou červěně vyznačeny dvě úhlopříčky. Jaký úhel svírají?
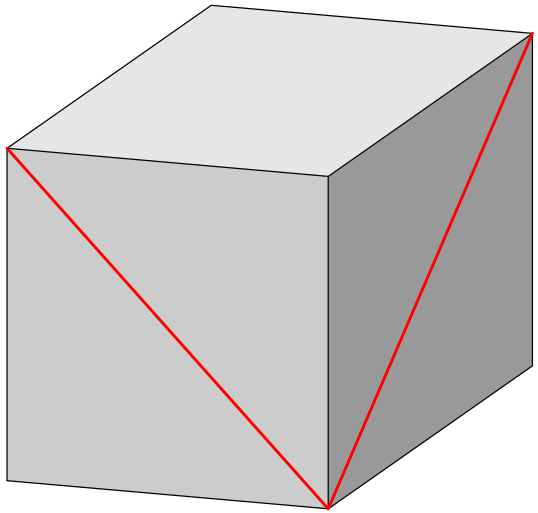
Řešení
Kolik jim je let?
Rodiče mají dvě děti. Otec je starší než matka, oba se znají již od dětství. Určete věk jednotlivých členů rodiny vyjádřený celými čísly, když víte, že součin jejich věků je $44\thinspace950$.Řešení
Hra s čepičkami
Představte si následující hru pro libovolně velkou skupinu účastníků. Každému nasadíme na hlavu buď černou nebo bílou čepičku tak, aby nevěděl, jakou barvu čepička má. Úkolem hráčů bude rozřadit se do dvou skupin tak, aby v jedné měli všichni bílé čepičky a ve druhé černé. Hráči spolu nesmějí mluvit, dávat si znamení ani jinak komunikovat. Mohou se však ještě před rozdáním čepiček domluvit. Poradíte jim vhodnou strategii?Řešení
Rozměry kašny
Kašna má tvar půkruhu přiléhajícího ke stěně, v jehož středu je půlkulatý sokl se sochou. Potřebujeme zjistit velikost kašny. Tomu, abychom změřili její poloměr, však překáží sokl uprostřed. Šikovný geometr si pomůže. Vyznačí si na stěně bod (bod $B$ na obrázku) ve výšce okraje kašny a ve vzdálenosti 50 cm od okraje kašny (bod $A$ na obrázku) a na okraji kašny vyznačí bod na kolmici ke stěně vedené z bodu $B$ (bod $C$ na obrázku). Změří, že vzdálenost mezi body $B$ a $C$ je 150 cm, a z toho vypočítá poloměr. Jak velký je poloměr kašny?

Řešení
Volební průzkum
V obci probíhají volby starosty, do kterých byli nominováni čtyři kandidáti: Anna, Břetislav, Cyril a Dorota. Všichni jsou napjatí, jak to dopadne, a tak místní kronikář dělá povolební průzkum tak, že každého z 250 voličů při východu nechá vyplnit dotazník se čtyřmi otázkami, na každou z nichž mají odpovědět buď "ano" nebo "ne":
Volil/a jste Annu?
Volil/a jste Břetislava?
Volil/a jste Cyrila?
Volil/a jste Dorotu?
Řešení
Honza a duchové
Honza jde vysvobodit princeznu ze zakletého zámku. Přijde na rozcestí, odkud vedou dál dvě cesty. Na rozcestí jsou tři duchové, z nichž jeden vždy mluví pravdu, jeden vždy lže a jeden někdy mluví pravdu a někdy lže. Honza smí položit jen dvě otázky - buď každou jinému duchovi, nebo obě jednomu z nich. Jak má postupovat, aby se od duchů dozvěděl, kterou cestou se má vydat? To není lehká otázka.Řešení
Ruská ruleta jinak
Ruská ruleta je hazardní hra, kde v sázce je život. Do šestikomorového bubínkového revolveru se vsune jeden náboj. Hráč válec roztočí, přiloží revolver ke spánku a zmáčkne spoušť. Šance na výhru, tj. na přežití, je samozřejmě $5:6$. Hru trochu pozměníme a revolver nabijeme dvěma náboji vloženými do sousedních komor a necháme na hráčích, jestli před zmáčknutím spouště bubínek roztočí nebo ne. Samozřejmě nebudeme hazardovat a budeme mířit na terč, ne na člověka. Představme si, že první hráč roztočil bubínek, zmáčkl spoušť a revolver nevystřelil. Jste další na řadě. Máte na výběr, jestli bubínek roztočíte nebo ne. Jak se rozhodnete?Řešení
Pohyblivé schody
Běhat po pohyblivých schodech v protisměru se zakazuje. My si však vyžádáme výjimečné povolení pro experiment nebo ho prostě uděláme myšlenkově. Představte si, že stoupáte rovnoměrným tempem po pohyblivých schodech a po 30 krocích vystoupáte nahoru. Potom se otočíte, po stejných schodech kráčíte stejným tempem dolů a po 70 krocích sestoupíte dolů. Kolik schodů byste museli vystoupat, kdyby se schody nepohybovaly?Řešení
Tři vypínače a tři žárovky
V rámci testu kreativního myšlení vám předloží uzavřenou bednu s víkem, na které jsou tři vypínače. Každý z nich zapíná jednu ze tří žárovek uvnitř bedny. Žárovky jsou vypnuté. Smíte vypínače jakkoli zapínat a vypínat, pak jednou otevřít víko a určit, který vypínač zapíná kterou žárovku. Kdyby tam byly dvě žárovky a dva vypínače, bylo by to prosté – jeden z nich zapneme, otevřeme víko a zjistíme, která žárovka svítí. Se třemi žárovkami však tato strategie nefunguje. Potíž je v tom, že každý vypínač má jen dvě polohy, takže pouhé polohy zapnuto a vypnuto nám poskytnou málo informace. Poradíte si s tím?Řešení
Japonský chrám
Tohle je další z historické sbírky japonských úloh san gaku. Lichoběžník $ABCD$ je opsán dvěma dotýkajícím se kružnicím $k_1$, $k_2$. Jeho základny mají délky $|AB|=2a$, $|CD|=2b$.
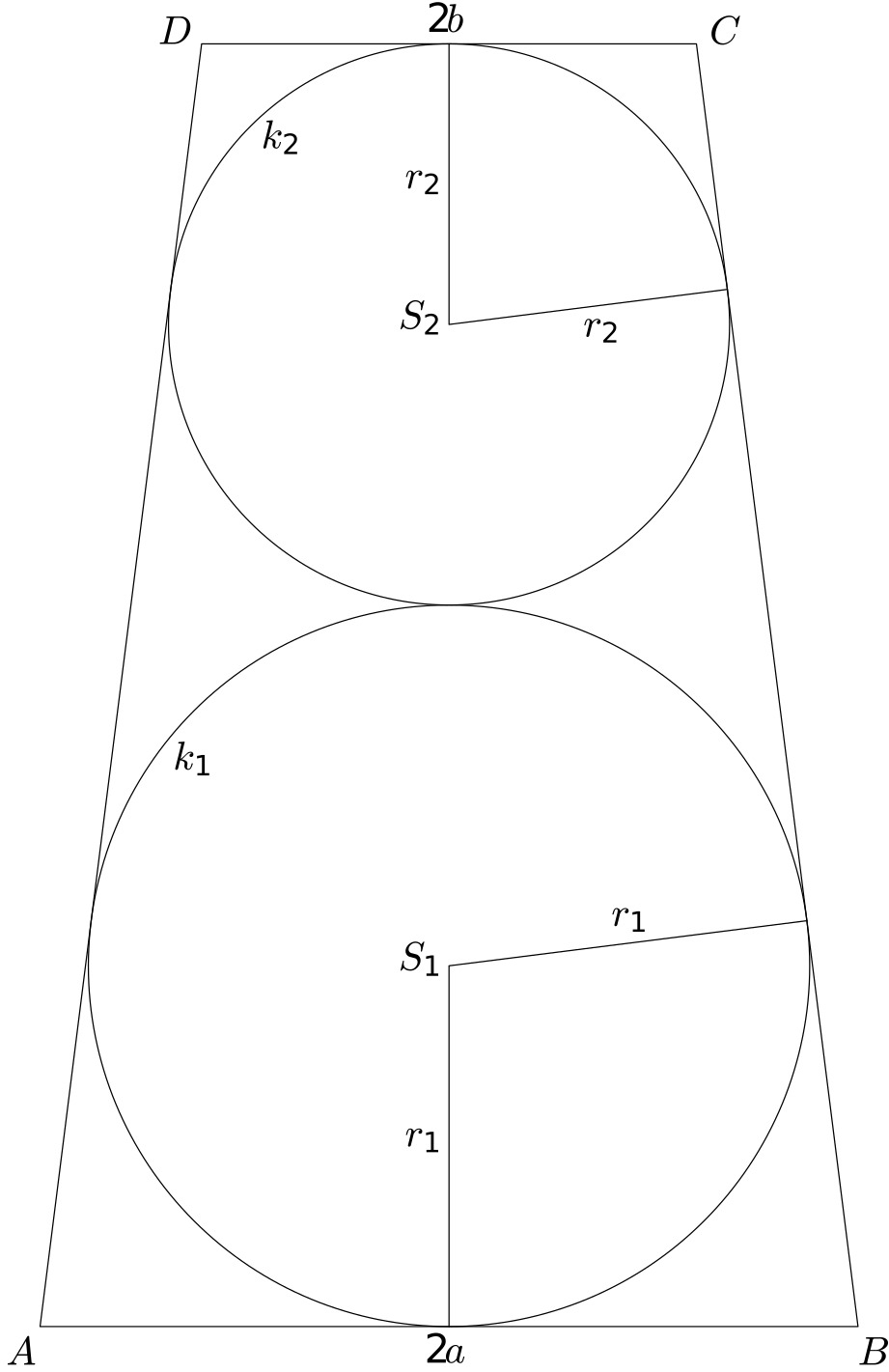
Řešení
Která číslice je na konci?
Existují "kouzelníci", kteří se živí tím, že na estrádách předvádějí bleskurychlé výpočty s velkými čísly. To zpravidla vyžaduje schopnost hlubokého soustředění, vynikající paměť, tvrdý trénink a znalost užitečných triků. Tato úloha je mnohem snazší, i když tak na první pohled nevypadá. Dokážete rychle určit poslední číslici součtu šestých mocnin čísel 111, 222, 333, 444, 555 a 666?Řešení
Čtyři turisté a visutý most
Každý jistě zná úlohu o vlku, koze a zelí, které je třeba přepravit bez úhony přes řeku. Naše úloha je trochu složitější.Čtyři turisté se vracejí za tmy po dlouhém celodenním výletu v horách a chtějí stihnout poslední autobus, který odjíždí přesně za hodinu. Od autobusu je dělí visutý most nad rozbouřenou řekou, který je úzký a ve velmi špatném stavu, unese jen dvě osoby a nedá se přejít potmě. Turisté mají jen jednu funkční svítilnu, dva z nich si ke všemu zvrtli kotník a mohou jít jen velmi pomalu. Nejrychlejší z turistů dokáže přejít most za 5 minut, druhý za 10 minut a ti zranění budou potřebovat 20, resp. 25 minut.
Mají turisté šanci stihnout autobus?
Řešení
Archimedova kruhová dvojčata
Je dána půlkružnice $k_1$ o poloměru $r_1$ a v ní dvě půlkružnice $k_2$, $k_3$ se středy ležícími na průměru půlkružnice $k_1$ a s poloměry $r_2$, $r_3$, jejichž součet se rovná $r_1$.
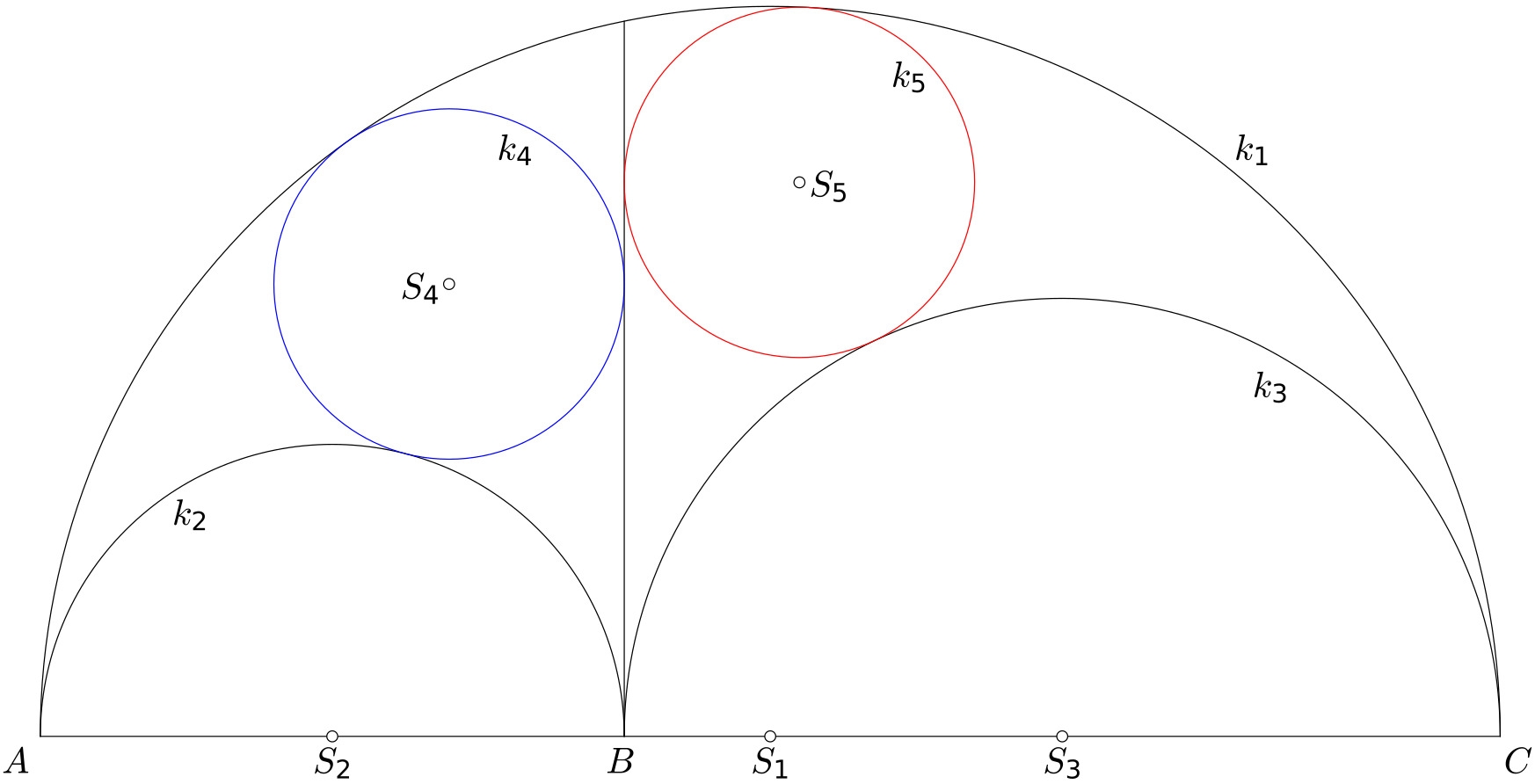
Úloha pochází z Archimedovy "Knihy lemat", která se dochovala v překladu, jejž pořídil arabský matematik a astronom Thabit Qurra ibn al-Ḥarrānī.
Řešení
Věk matematikových děti ještě jinak?
Už jsme se jednou setkali s matematikem, který se bavil tím, že nechal kolegu uhodnout věk jeho tří dětí. Zde je jiná varianta."Mám tři děti, součin jejich věků vyjádřených celými čísly je 36, součet odpovídá přesně číslu dnešního dne v měsíci," pochlubí se kolegovi.
"To je nedostatečná informace."
"Ano. Nejstarší z nich je syn."
Jak staré jsou děti?
Řešení
Expedice přes poušť
Velitel připravuje cestu expedice přes poušť. Ví, že k jejímu překonání budou potřebovat šest dnů. Může si obstarat jakékoli množství jídla a pití, výprava však najednou unese zásoby jen na čtyři dny. Jak je třeba cestu naplánovat a kolik zásob jídla a pití celkem bude expedice potřebovat?Řešení
Lichoběžník a kružnice
Délky základen rovnoramenného lichoběžníku $ABCD$ jsou v poměru $|AB|:|CD|=3:2$. Kružnice sestrojená nad průměrem $AB$ protíná základnu $CD$ tak, že její část ležící uvnitř kružnice má délku ${1\over2}|CD|$.
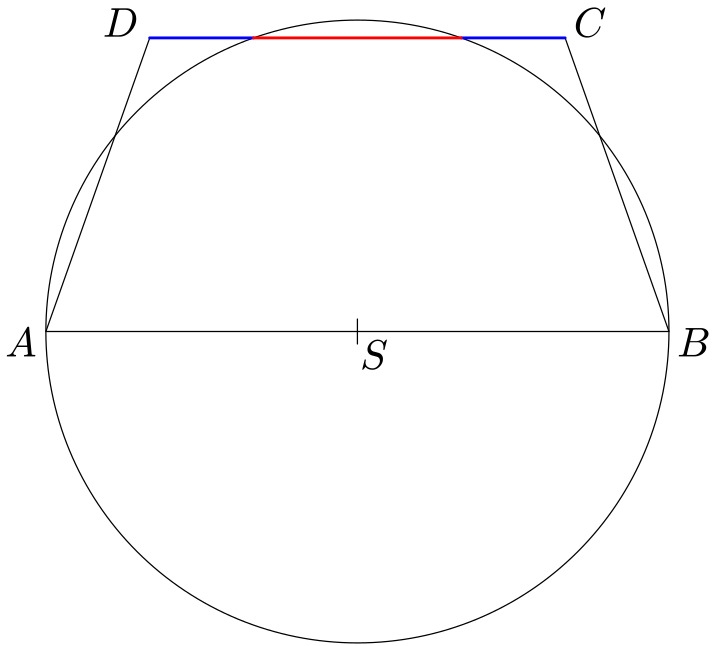
Řešení
Velká a malá ručička na hodinách
Starší řidiči si jistě pamatují poučku z autoškoly, že při řízení mají být ruce na volantu v poloze "za deset minut dvě" nebo "deset deset". U dnešních menších volantů s posilovačem řízení se za optimální z hlediska bezpečnosti považuje poloha "tři čtvrtě na tři". To jsou ovšem jen symbolické, přibližné instrukce. Podle nich by totiž obě ruce nebyly ve stejné výšce. Existuje vůbec postavení hodinových ručiček symetrické podle svislé osy? Jaký čas v takovém okamžiku hodiny ukazují? Předpokládejme, že ručičky neposkakují, pohybují se rovnoměrným pohybem.Řešení
Jsou v Praze dva lidé se stejným počtem vlasů?
Řešení
Čtverec a trojúhelník v kruhu
Ke čtverci o straně délky $a$ přiléhá rovnostranný trojúhelník, jak je znázorněno na obrázku. Určete velikost poloměru kružnice $k$ opsané tomuto obrazci.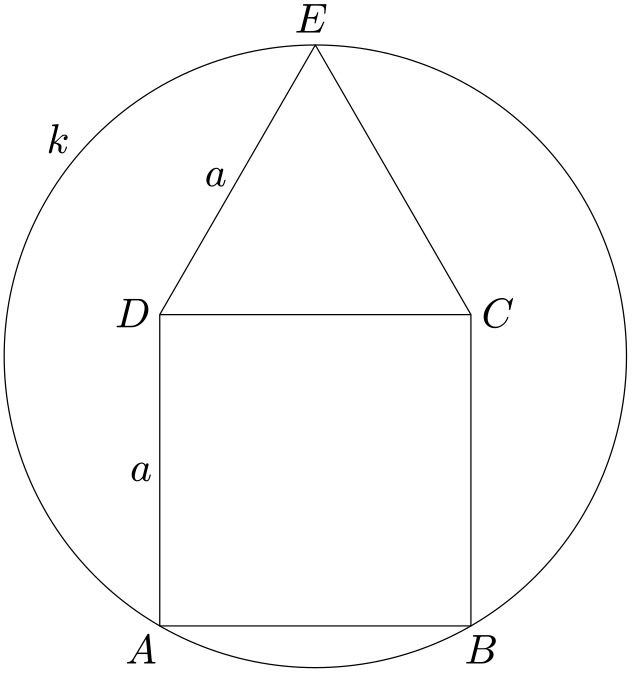
Řešení
Přesýpací hodiny
Odměřte 15 minut pomocí dvou přesýpacích hodin, z nichž jedny odměřují 7 minut a druhé 11 minut. Dokážete to jen trojím obrácením hodin?Řešení
Kolik je třem dětem let?
Dva matematici, kteří přijeli na konferenci, se po letech potkají na chodbě hotelu a dají se do hovoru.Karel: "Dlouho jsme se neviděli. Víš, že mám tři děti?"
Pierre: "To je pěkné. Kolik jim je let?"
Karel: „No, to snadno zjistíš. Součin jejich věku je 36 a součet jejich věku je stejný jako číslo tohoto patra."
Pierre po krátkém zamyšlení: "Tato informace mi nestačí."
Karel: "Máš pravdu. Nejstarší dítě je syn."
Pierre: "Aha, tak teď už vím, kolik jim je let."
Jak staré jsou Karlovy děti?
Řešení
Tangens vnitřních úhlů v trojúhelníku
Může být tangens každého ze tří vnitřních úhlů trojúhelníku kladné celé číslo? Jaký tvar má takový trojúhelník?Řešení
Měření času doutnákem
Máte jeden doutnák a krabičku zápalek. Víte jen to, že doutnák po zapálení na jednom konci dohoří přesně za minutu. Doutnák však může hořet nepravidelným tempem. Jak odměříte 15 sekund? (Úloha má teoretické řešení, realizovat ho v praxi nemusí být možné.)Řešení
Dcery a synové
Uvažujme všechny rodiny se dvěma dětmi, z nichž jedno je dcera. Pro jednoduchost předpokládejme, že se v populaci rodí stejné množství chlapců jako dívek. S jakou pravděpodobností mají v těchto rodinách i syna?Řešení
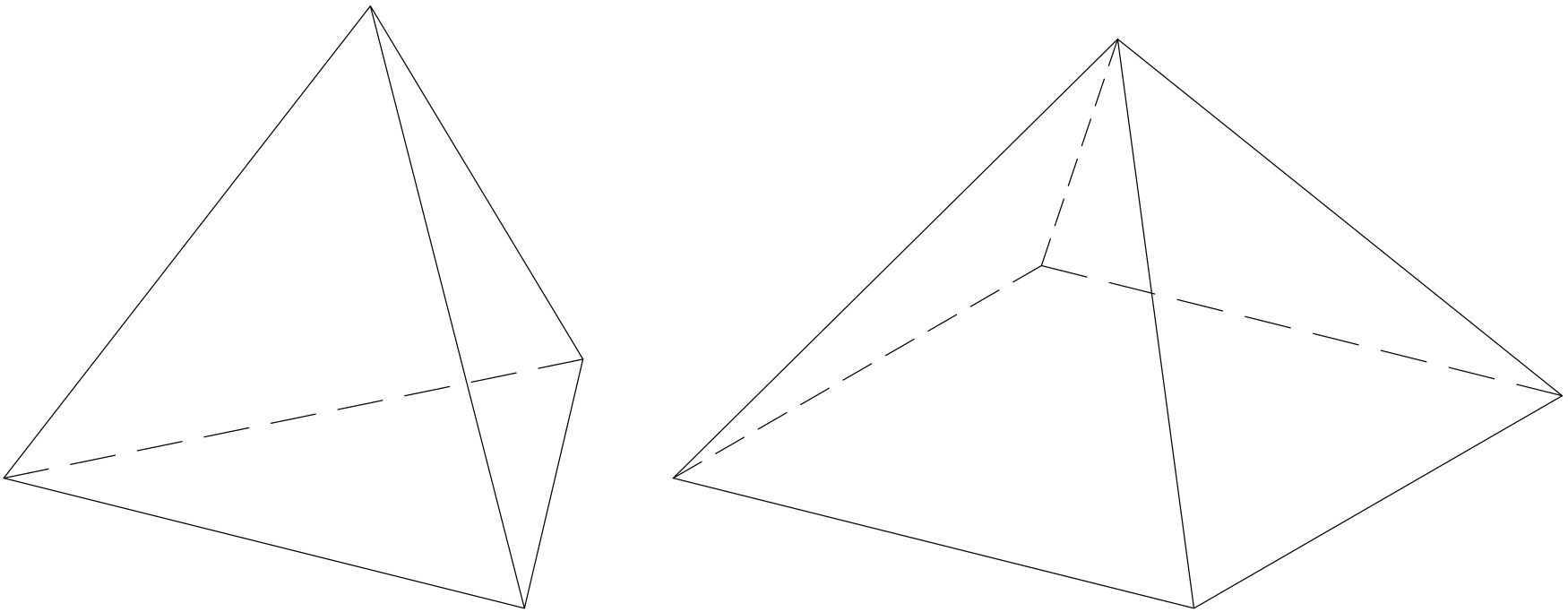
Dva jehlany
Uvažujme dva jehlany. Jeden má trojúhelníkovou podstavu, druhý čtvercovou. Všechny hrany obou jehlanů mají stejnou délku.
Řešení
Souboj pěti gangsterů
Pět gangsterů vyjde před putyku, aby si spolu vyřídili účty. Postaví se tak, že vzdálenost mezi každými dvěma z nich je jiná. Každý zamíří na toho nejbližšího a všichni na povel najednou vystřelí. Nejméně jeden z nich souboj přežije. Umíte to vysvětlit?Řešení
Jak sečíst 999 zlomků?
Určitá míra lenosti je užitečná. Než se pustíme do na první pohled úmorného počítání, je dobré se napřed zamyslet. O brzké genialitě jednoho z největších matematiků Carla Friedricha Gausse se traduje, jak jeho učitel chtěl na chvíli zabavit žáky a dal jim sečíst přirozená čísla od jedné do sta. Mladý Gauss ho překvapil téměř okamžitou odpovědí. Místo mechanického sčítání dlouhé řady čísel si uvědomil, že když čísla seřadí do sloupce a napíše vedle nich čísla v opačném pořadí, bude součet v každém řádku 101, a tedy součet čísel v jednom sloupci bude $101\cdot100\cdot{1\over2}=5050$. Přijdete na to, jak rychle sečíst řadu zlomků ${1\over1\cdot2}+{1\over2\cdot3}+{1\over3\cdot4}+\dots+{1\over998\cdot999}+{1\over999\cdot1000}$?Řešení
Dvě věže
Dvě válcové věže mají stejnou výšku, ale různý poloměr. Kolem každé věže se od paty po horní ochoz vine výstupní rampa, která má v obou případech stejný stálý sklon. Po které rampě při výstupu na věž ujdeme větší vzdálenost?Řešení
Kdo z těch čtyř mluví pravdu?
Čtyři chlapíci o sobě vědí, že každý z nich buď vždy říká pravdu, nebo vždy lže. Na otázku, kolik je mezi nimi lhářů, odpovědí:
První: "Jeden z nás lže."
Druhý: "Dva z nás lžou."
Třetí: "Tři z nás lžou."
Čtvrtý: "Všichni čtyři lžeme."
Řešení
Čtyři děti
Novomanželé Jan a Jana plánují založení rodiny. Chtěli by mít čtyři děti. Jana si dělá trochu starosti: "A co když to budou čtyři kluci nebo čtyři holky?" Jan ji chlácholí: "To je sice možné, ale málo pravděpodobné. Pokud předpokládáme, že se dívky a chlapci rodí stejně často, pak nejpravděpodobnější sestava je dva kluci a dvě holky." Má pravdu?Řešení
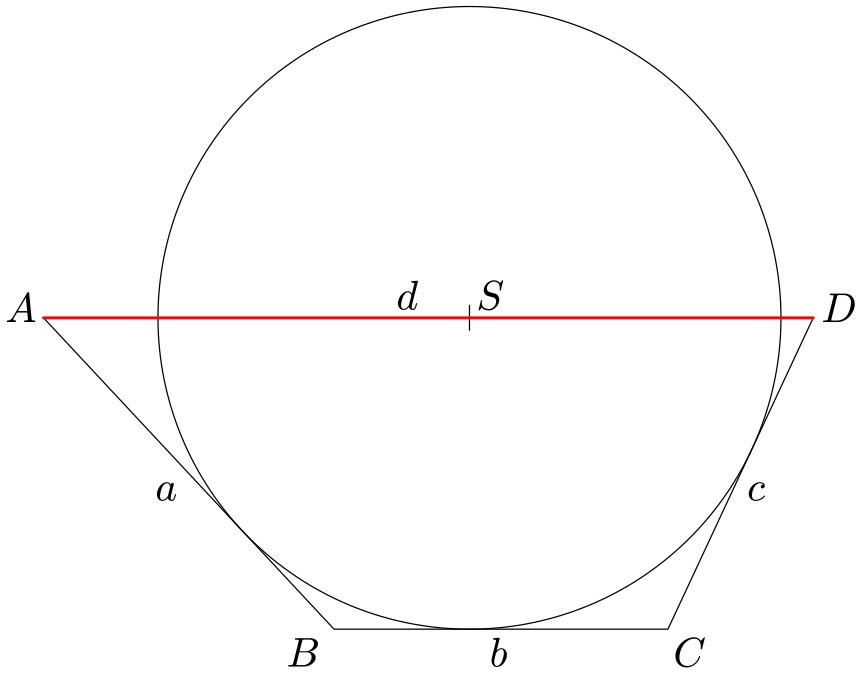
Půlkruh v lichoběžníku
Lichoběžník $ABCD$ má tu vlastnost, že střed kružnice dotýkající se základny $BC$ a ramen $AB$, $CD$ leží na základně $CD$. Určete délku základny $|CD|=d$, jsou-li dány délky ramen $|AB|=a$, $|CD|=c$.
Řešení
Diplomatická pošta
Agent pracující na vyslanectví chce poslat do centrály citlivé dokumenty. Protože ví, že kontrarozvědka tajně otvírá diplomatickou poštu, pořídí si bezpečnostní schránkou s visacím zámkem, od kterého má klíč pouze on. Poslat klíč by nebylo bezpečné. Jak to ve spolupráci s centrálou provede, aby dokumenty doručil s jistotou, že je nikdo nepovolaný neviděl? (Jde o logickou úvahu, nehledejte násilná řešení ve stylu bondovek. Předpokládejte, že schránku ani zámek nelze otevřít jinak než použitím klíče.)Řešení
Kolik je dětem let?
Dva matematici, kteří přijeli na konferenci, se po letech potkají na chodbě hotelu a dají se do hovoru.Karel: "Dlouho jsme se neviděli. Víš, že mám tři děti?"
Pierre: "To je pěkné. Kolik jim je let?"
Karel: „No, to snadno zjistíš. Součin jejich věku je 36 a součet jejich věku je stejný jako číslo tohoto patra."
Pierre po krátkém zamyšlení: "Tato informace mi nestačí."
Karel: "Máš pravdu. Nejstarší dítě je syn."
Pierre: "Aha, tak teď už vím, kolik jim je let."
Jak staré jsou Karlovy děti? Věk dětí je samozřejmě vyjádřen celými čísly.
Řešení
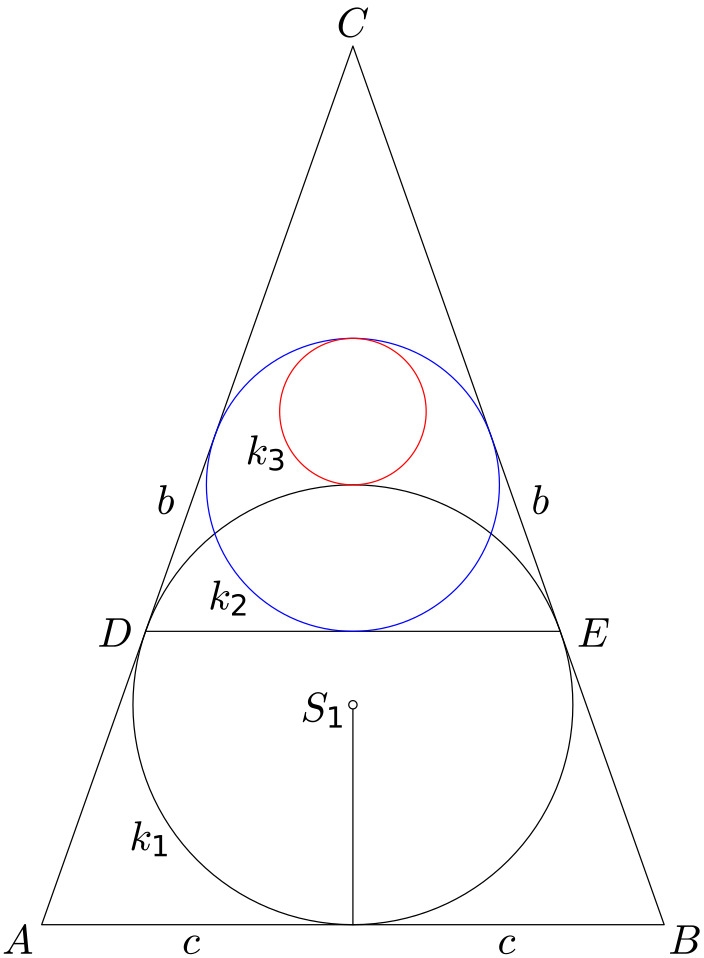
San gaku 1
San gaku jsou japonské geometrické úlohy a tvrzení, které byly během éry Edo v 17. až 19. století malovány na dřevěné desky a věnovány šintostickým svatyním a budhistickým chrámům jako oběť nebo jako úlohy pro mnichy. Toto je příklad:Mějme rovnoramenný trojúhelník $ABC$ s délkami stran $b=|AC|=|BC|$ a $2c=|AB|$. Trojúhelník má vepsanou kružnici $k_1$ o poloměru $r_1$, která se dotýká stran $AC$, $BC$ trojúhelníku v bodech $D$, $E$. Trojúhelníku $DEC$ je obdobně vepsána kružnice $k_2$ o poloměru $r_2$. Kružnice $k_3$ o poloměru $r_3$ se dotýká obou kružnic $k_1$, $k_2$ (viz obrázek).
Řešení
Džbán a dvě sklenice
Máte džbán s vodou, do kterého se vejde víc než 1 l vody, a dvě sklenice o objemu 0,5 l a 0,2 l. Vaším úkolem je vodu ze džbánu rozlít do sklenic tak, aby v každé z nich bylo přesně 0,2 l vody.Řešení
Zbytky při dělení
Najděte nejmenší celé kladné číslo, které při dělení 2 dá zbytek 1, při dělení 3 dá zbytek 2, při dělení 4 dá zbytek 3, při dělení 5 dá zbytek 4, při dělení 6 dá zbytek 5, při dělení 7 dá zbytek 6, při dělení 8 dá zbytek 7, při dělení 9 dá zbytek 8, při dělení 10 dá zbytek 9 a při dělení 11 dá zbytek 10.Řešení
Prádelní šňůry
Na dvoře jsou čtyři kůly pro sušení prádla uspořádané do čtverce. Děti si hrály s prádelní šňůrou, natáhly ji od tří kůlů doprostřed a svázaly tak, jak je na obrázku vyznačeno modrými čarami. Tři úseky šňůry od kůlů k uzlu uprostřed jsou dlouhé $a$, $b$, $c$.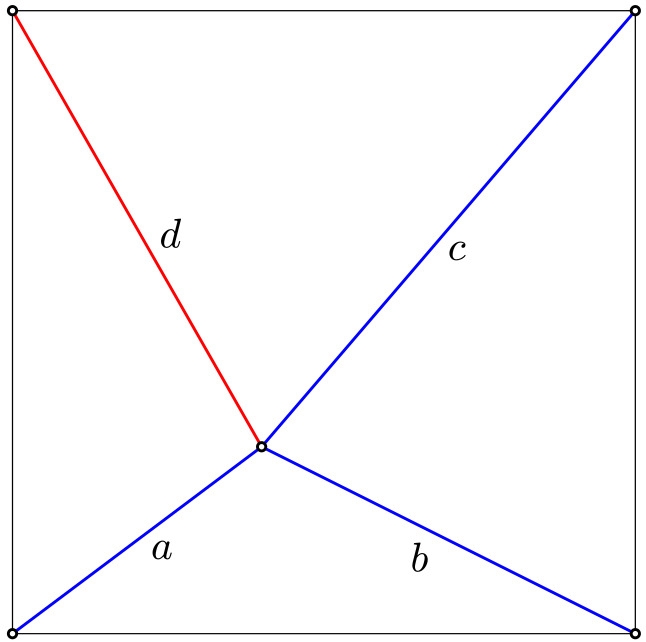
Řešení
Poutník na rozcestí
Poutník přijde na rozcestí, z něhož vedou cesty ke dvěma městům, o kterých je známo, že v jednom žijí lidé, kteří vždy říkají pravdu, a ve druhém lidé, kteří vždy lžou. Na rozcestí potká člověka z jednoho z těch dvou měst. Jakou otázku mu položí, aby se bezpečně dozvěděl, do kterého města která cesta vede?Řešení
Sultánův poklad
Sultán měl 6 synů. Měl také palác s mnoha sklepními kobkami, ve kterých byl ukryt poklad. V každé kobce bylo tolik truhlic, jako kobek v paláci. Každá truhlice obsahovala tolik zlaťáků mincí, kolik truhlic bylo v kobce. Sultán si zavolal pokladníka a řekl mu, že dostane jednu truhlici se zlaťáky, když dokáže rozdělit zbývající poklad svým 6 synům rovným dílem. Když to nedokáže, přijde o hlavu. Jakou šanci měl pokladník, že si zachrání život a získá truhlici se zlaťáky?Řešení
Jak spravedlivě rozdělit dort?
Anička, Bětka a Cecilka dostaly dort a chtějí si ho spravedlivě rozdělit. Kdyby jedna z nich dort rozkrájela a každá by si jednoduše vzala jeden kus, mohla by si některá z nich myslet, že všechny kusy nebyly stejně velké a na ni zbyl ten nejmenší. Jak mají postupovat, aby si žádná z nich nemohla právem stěžovat, že dostala méně než třetinu dortu?Řešení
Neposedný pes
Muž pracuje 10 km od domova a vrací se z práce domů na kole. Ve stejném okamžiku, kdy vyráží na cestu domů, jeho mu žena vychází pěšky naproti se svým psem. Muž jede rychlostí 15 km/h, žena jde rychlostí 5 km/h. Pes, který běhá rychlostí 20 km/h, okamžitě vyrazí pánovi naproti. Jakmile k němu doběhne, otočí se a běží zpět ke své paní. Když k ní dorazí, běží opět k pánovi. To se opakuje až do okamžiku, kdy se muž se ženou potkají. Kolik toho pes celkem naběhá?Řešení
Doutnáky
Máte dva doutnáky a zapalovač. Víte jen to, že každý z doutnáků po zapálení na jednom konci dohoří přesně za minutu. Doutnák může hořet nepravidelným tempem. Jak pomocí těch dvou doutnáků odměříte 45 sekund?Řešení
S jakou pravděpodobností je druhé z dětí dcera?
Předpokládejme, že chlapci se rodí se stejnou pravděpodobností jako dívky, a uvažujme všechny rodičovské páry, které mají dvě děti, z nichž jedno je syn. Jaká je pravděpodobnost, že náhodně vybraný takový pár má i dceru?Řešení
Přijdou tři logici do baru
Přijdou tři logici do baru a když je barman osloví otázkou "Všichni pivo, pánové?", první ihned odpoví: "Nevím". Druhý také hned řekne: "Nevím". Třetí se po chvilce přemýšlení rozzáří a řekne: "Ano". Asi jste se někdy setkali se situací, kdy na dotaz typu "Půjdeme do kina nebo zůstaneme doma?" partner odpoví "Ano!" a tázajícího uvede do rozpaků nebo ho přímo rozčílí. Barman však nezaváhal a splnil objednávku. Co hostům nalil a proč?Řešení
Falešné mince
Král se dozvěděl, že se ho mincmistr pokusil ošidit a vyrobil celý pytel mincí, které váží o 1 gram méně než předepsaných 10 gramů. Nechal z mincovny přinést všechny pytle s vyrobenými mincemi, předvolal si mincmistra a řekl mu, že když nedokáže jedním vážením zjistit, v kterém pytli jsou ty lehčí mince, bude popraven. Jak si mincmistr zachrání život?Řešení
Trik se třemi kartami
Představte si, že vás někdo vyzve, abyste si s ním zahráli následující hru. Ukáže vám tři speciální dvoustranné karty. Jedna má na obou stranách pik, druhá má na jedné straně pik a na druhé káro, třetí má na obou stranách káro: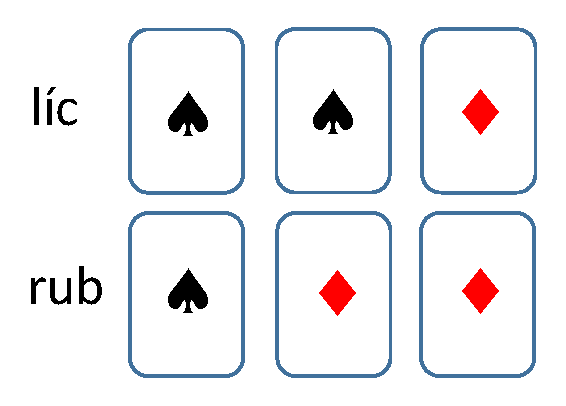
Řešení
Čaj s mlékem
Mám dvě stejné sklenice, jedna je zčásti naplněna čajem, druhá obsahuje stejné množství mléka. Ze sklenice s mlékem odleju trochu do sklenice s čajem a zamíchám. Pak odleju ze směsi čaje s mlékem do sklenice s mlékem tolik, aby v obou sklenicích bylo stejné množství tekutiny. V první sklenici je tedy čaj zředěn mlékem, ve druhé sklenici je mléko zředěno čajem. Je v první sklenici více mléka než čaje ve druhé sklenici, nebo je naopak ve druhé sklenici více čaje než mléka v první?Řešení
Černé a bílé čepičky
Učitel matematiky procvičuje logické myšlení. Vyvolá tři žáky a ukáže jim tři černé a dvě bílé čepičky. Pak jim řekne, aby zavřeli oči, nasadí každému jednu čepičku na hlavu a zbývající dvě schová. Pak je vyzve, aby otevřeli oči a řekli, jakou barvu má čepička na jejich vlastní hlavě. Po chvíli uvažování jeden z nich zvedne ruku a oznámí barvu své čepičky. Jakou barvu měla jeho čepička a jak na to přišel?Řešení
Dva prstence
Z hliníkové koule o průměru 20 mm uděláme prstenec tak, že do ní přesně jejím středem vyvrtáme otvor takovým způsobem, aby výška prstence byla 10 mm. Pak stejným způsobem uděláme prstenec o výšce 10 mm z hliníkové koule o průměru 40 mm. Který z prstenců bude vážit víc?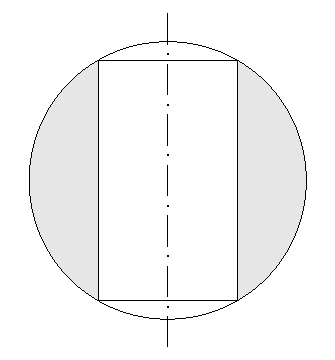
Řešení
Jak rozlámat tabulku čokolády?
Tabulka čokolády se skládá ze $4 \cdot 6 = 24$ čtverečků. Pokud ji chcete úplně rozdělit na 24 samostatných čtverečků, můžete postupovat různými způsoby. Například můžete nejprve pěti lomy vytvořit 6 čokoládových proužků po 4 kusech. Chcete-li získat jednotlivé čtverečky, musíte rozlomit každý z těchto proužků třikrát. Celkem uděláte $5 + 3 \cdot 6 = 23$ lomů. Je možné to zvládnout s méně než 23 lomy obratnějším postupem (bez toho, že byste lámali několik kusů čokolády najednou)?Řešení
Barevné koule
U přijímacího pohovoru vám ukážou tři krabice. Řeknou vám, že v jedné krabici jsou jen zelené koule, ve druhé jsou jen modré koule a ve třetí jsou zelené i modré koule. Na jedné krabici je napsáno „zelené“, na druhé „modré“ a na třetí „zelené a modré“. Nápis ani na jedné krabici však neodpovídá obsahu. Máte za úkol určit, co je v které krabici, ale smíte sáhnout jen do jedné krabice a vytáhnout z ní jen jednu kouli. Dokážete to?Řešení
Fotbal a narozeniny
Odhadovat pravděpodobnost nějakého jevu je často ošidné. Oblíbeným příkladem je otázka, s jakou pravděpodobností se v určité skupině lidí vyskytují dva, kteří mají narozeniny ve stejný den. Jak je tomu např. v případě dvou fobalových mužstev na hřišti? Vsadili byste si na to, že dva z hráčů mají narozeniny ve stejný den?Řešení
Prodloužený provaz
a) Kolem válce o průměru 10 cm obtočíme provaz a vyznačíme na něm délku obvodu válce. Vezmeme provaz o 1 m delší a vytvoříme z něj kruh kolem válce tak, aby byl od válce všude ve stejné vzdálenosti. Jak daleko od válce provaz bude?b) Představme si, že bychom totéž dokázali udělat se Zeměkoulí na rovníku. O kolik by se prodloužený provaz zvedl na zem? Podlezla by ho kočka?
Řešení
Spojování řetězu
Máte šest kusů řetězu, každý o pěti článcích. Jaký nejmenší počet článků je třeba rozříznout a opět svařit, abyste získali uzavřený kruhový řetěz o třiceti článcích?Řešení
Hippokratovy měsíčky
Snad každý zná jméno velkého řeckého matematika Eukleida (asi 325 př. n. l. – asi 260 př. n. l.), autora slavných Základů, nejúspěšnější knihy o matematice v historii. Méně je znám jeho předchůdce z 5. stol. př. n. l., Hippokratés z Chiu, který rovněž shrnul soudobé geometrické poznatky v knize Základy. Ta se téměř celá ztratila, informace o Hippokratově geometrii čerpáme především od jeho následovníků. Hippokratés je autorem pěkné úlohy, které se říká Hippokratovy měsíčky: Do půlkruhu vepišme pravoúhlý trojúhelník, jehož přeponou $c$ je průměr půlkruhu. (Podle Thaletovy věty leží třetí vrchol u pravého úhlu na oblouku půlkruhu.) Nad každou z odvěsen $a$, $b$ sestrojme půlkruh vně trojúhelníku. Tři půlkružnice vymezí dva Hippokratovy měsíčky. Určete velikost jejich celkové plochy. Hippokratés to dokázal před 2500 lety!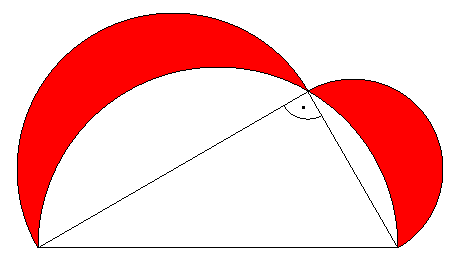
Řešení
10 loupežníků
Tlupa deseti loupežníků chce ukrýt uloupený poklad do truhlice. Protože si samozřejmě navzájem nedůvěřují, náčelník rozhodne, že se truhlice musí zajistit visacími zámky tak, aby se dala otevřít, jen když se u toho sejdou aspoň čtyři loupežníci. Kolik různých zámků na truhlici budou muset pověsit a kolik klíčů budou potřebovat?Řešení
Na jih, na východ, na sever a zpět
Člověk vyrazí na jih, po jednom kilometru zahne na východ, po dalším kilometru zahne na sever a octne se ve výchozím bodu. Kde na Zemi je takový výchozí bod?Řešení
O pomalejšího koně
Král zavolá své dva syny a oznámí jim, že království po něm převezme ten, jehož kůň urazí vzdálenost do sousedního města za delší dobu. Kralevicové sednou na své koně a záměrně je zadržují, aby jeden nepředběhl druhého. Brzy zjistí, že takhle do cíle nikdy nedojedou. Kolem jde mudrc a ptá se, proč se tváří tak zoufale. Když mu vysvětlí situaci, mudrc jim řekne, aby sesedli s koní, a chvíli s nimi rozmlouvá. Nato oba nasednou na koně, a co nejrychleji uhánějí k sousednímu městu. Co jim mudrc poradil?Řešení
Káva s mlékem
Mám šálek černé kávy. Upiju z něj 1/6 a doleju mlékem. Upiju 1/3 a doleju mlékem. Upiju 1/2, doleju mlékem a vypiju celý šálek. Kolik kávy a kolik mléka jsem vypil?Řešení
Dělení pozemku
K pozemku tvaru ostroúhlého trojúhelníku ABC vede přístupová cesta, která ústí v bodě P ležícím na straně AB, blíž k bodu B. Majitel chce pozemek rozdělit mezi dva syny tak, aby obě části měly stejný obsah, aby obě byly přístupné z přístupové cesty a aby dělicí hranice byla přímá. Hranice tedy bude tvořena úsečkou PQ, kde Q je vhodný bod na straně AC. Umíte najít polohu bodu Q konstrukcí bez výpočtu?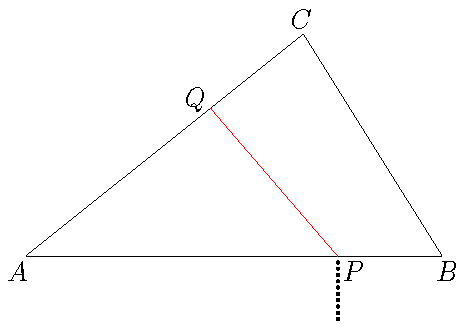
Řešení
Kdo rozbil okno?
Ve škole někdo rozbil okno. Školník zadržel čtyři chlapce, kteří v té době byli na dvoře. Tři z nich jsou notoričtí lháři, jen jeden mluví pravdu. Toto jsou jejich výpovědi:
Adam: "Já jsem okno nerozbil."
Béďa: "Adam lže."
Cyril: "Béďa lže."
David: "Okno rozbil Béďa."