Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Dělení trojúhelníkové parcely
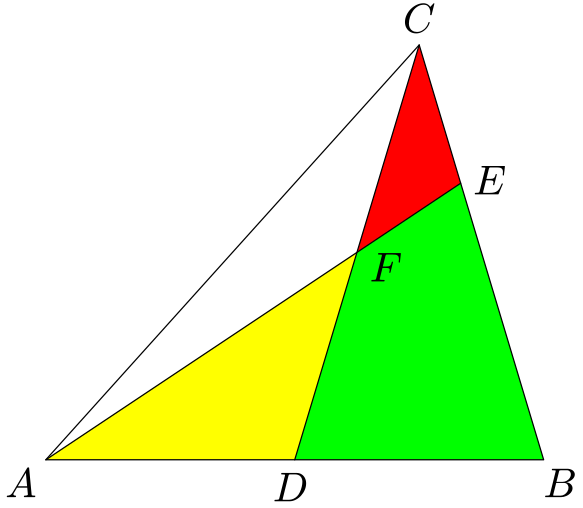
Trojúhelníková parcela $ABC$ o obsahu $10\,{\rm ha}$ je rozdělena dvěma přímými hranicemi $CD$ a $AE$ na čtyři části:
Bod $D$ je uprostřed strany $AB$, bod $E$ je uvnitř strany $BC$. Trojúhelníková část $AFC$, kde $F$ je průsečík úseček $CD$ a $AE$, má obsah $4\,{\rm ha}$. Jak velké jsou obsahy ostatních tří částí parcely?
Řešení
Označme obsahy trojúhelníků $ADF$, $FEC$, $DBF$, $BEF$ po řadě $a$, $b$, $c_1$, $c_2$ (jednotky ha budeme ve výpočtu vynechávat):
Protože trojúhelníky $ADF$, $DBF$ mají stejně dlouhé strany $AD$, $DB$ a stejnou výšku z vrcholu $F$, mají i stejný obsah: $a=c_1$. Ze stejného důvodu mají stejný obsah trojúhelníky $ADC$, $DBC$, takže $a+4=c_1+c_2+b=5$, tj. $a=c_1=1$ a $b=4-c_2$. Označíme-li $v_1$ a $v_2$ výšky trojúhelníků $BEF$ a $BEA$ spuštěné z vrcholů $F$ a $A$, pak platí $c_2:(a+c_1+c_2)=v_1:v_2=b:(b+4)$, tj. $c_2:(2+c_2)=(4-c_2):(8-c_2)$. Odtud vypočteme $c_2={4\over3}$, $b={8\over3}$. Hledané obsahy částí parcely tedy jsou $a=1\,{\rm ha}$, $b={8\over3}\,{\rm ha}$ a $c_1+c_2={7\over3}\,{\rm ha}$.