Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Čtverec a trojúhelník v kruhu
Ke čtverci o straně délky $a$ přiléhá rovnostranný trojúhelník, jak je znázorněno na obrázku. Určete velikost poloměru kružnice $k$ opsané tomuto obrazci.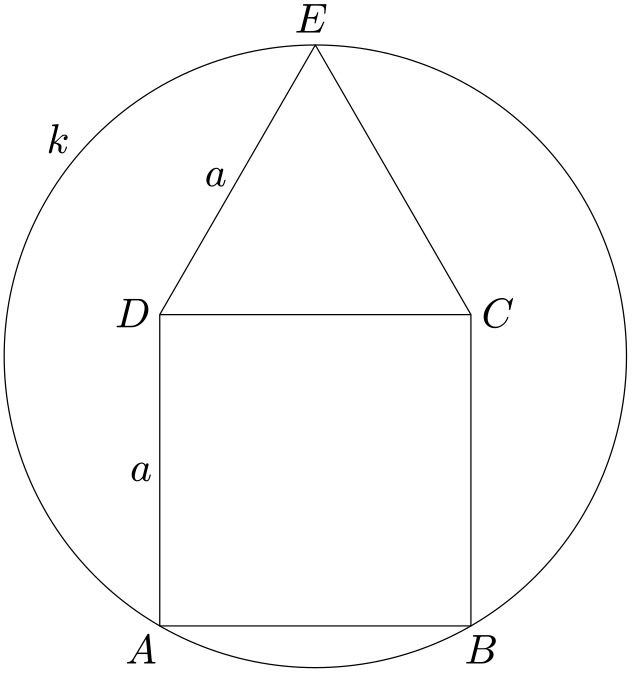
Řešení
Poloměr $r$ kružnice $k$ můžeme určit výpočtem s použitím věty o tětivách, kterou ve svých Základech uvádí již Eukleides.
Úlohu lze však řešit jednodušeji geometrickou úvahou: Uvnitř čtverce sestrojíme rovnostranný trojúhelník $ABS$. Protože úsečku $AS$ a $DE$ jsou rovnoběžné a mají stejnou délku, čtyřúhelník $ASED$ je rovnoběžník, takže i úsečky $SE$ a $AD$ mají stejnou délku. Bod $S$ je tedy středem kružnice $k$.
