Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Dvě tětivy

V kružnici $k$ zvolíme dvě tětivy $AB$, $DE$ tak, že tětiva $DE$ protíná tětivu $AB$ v jejím středu $C$. Nad tětivou $DE$ sestrojíme půlkružnici vně kružnice $k$ a na této půlkružnici sestrojíme bod $F$ tak, že přímky $CF$ a $DE$ jsou navzájem kolmé.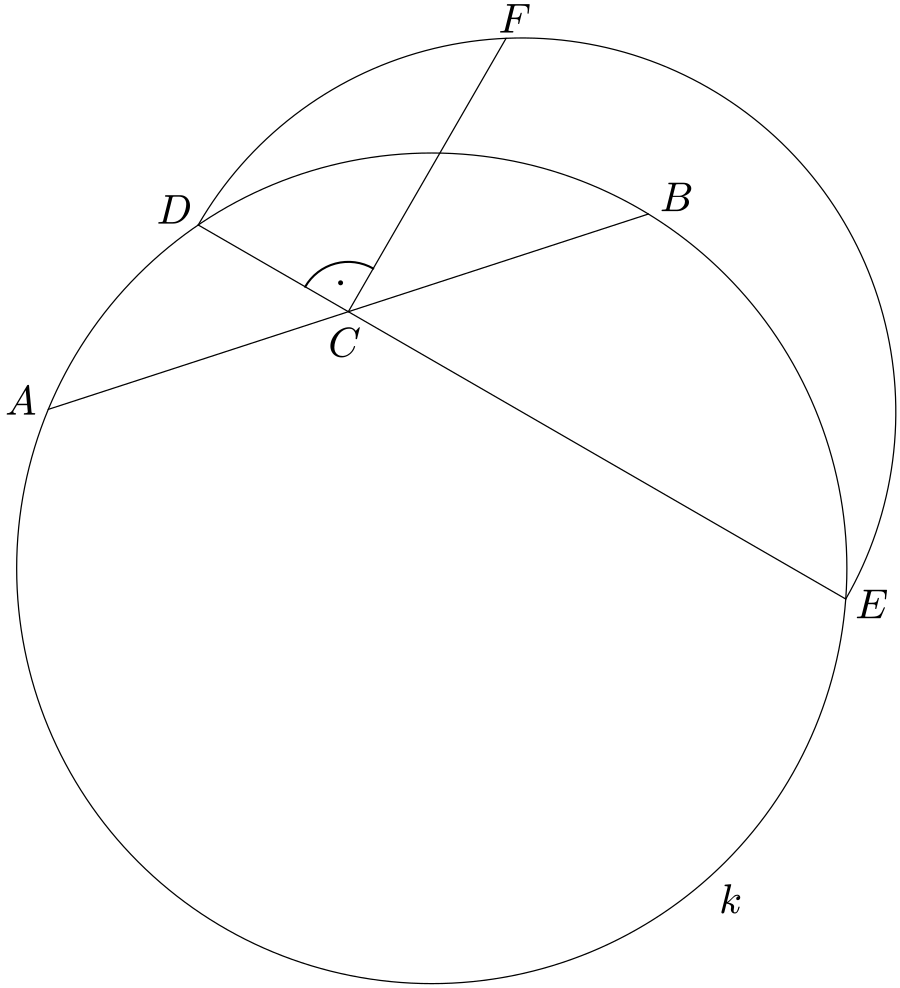

Dokažte, že úsečky $AC$ a $CF$ jsou stejně dlouhé.

Řešení

Z věty o mocnosti bodu ke kružnici plyne, že pro dvě protínající se tětivy v kružnici platí vztah $|AC|\cdot|CB|=|DC|\cdot|CE|$.

Kdo o mocnosti bodu ke kružnici neslyšel, může si to snadno dokázat sám:

Úhly $ACD$, $BCE$ jsou shodné, a shodné jsou i úhly $EDA$, $EBA$, protože jsou to úhly nad tětivou $AE$. Z toho plyne, že trojúhelníky $ACD$, $ECB$ jsou podobné, takže platí ${|AC|\over|CE|}={|DC|\over|CB|}$, tj. $|AC|\cdot|CB|=|DC|\cdot|CE|$. (Všimněte si, že to platí obecně, nepotřebovali jsme vědět, že bod $C$ je středem úsečky $AB$.) Podle Thaletovy věty je trojúhelník $DEF$ pravoúhlý a pro jeho výšku $CF$ podle Eukleidovy věty o výšce platí $|CF|^2=|DC|\cdot|CE|$. (Tento vztah opět snadno dokážeme z podobnosti pravoúhlých trojúhelníků $DCF$, $FCE$.) Odtud již dostaneme $|CF|^2=|DC|\cdot|CE|=|AC|\cdot|CB|=|AC|^2$, tj. $|CF|=|AC|$.