Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Barevné tětivy
Na kružnici zvolíme 6 různých bodů a každé dva spojíme modrou nebo červenou úsečkou tak, že vznikne právě jeden červený a právě jeden modrý trojúhelník. Např. takto: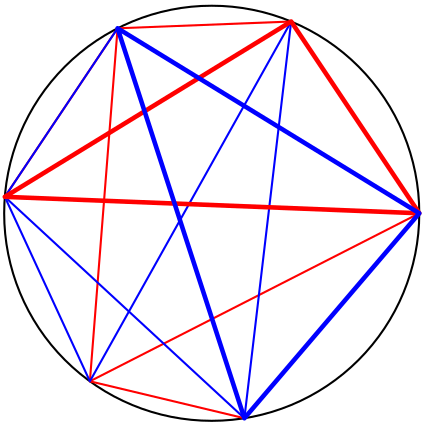
Řešení
Vrcholy červeného trojúhelníku označíme 1, 2, 3 a zbývající vrcholy 4, 5, 6.