Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
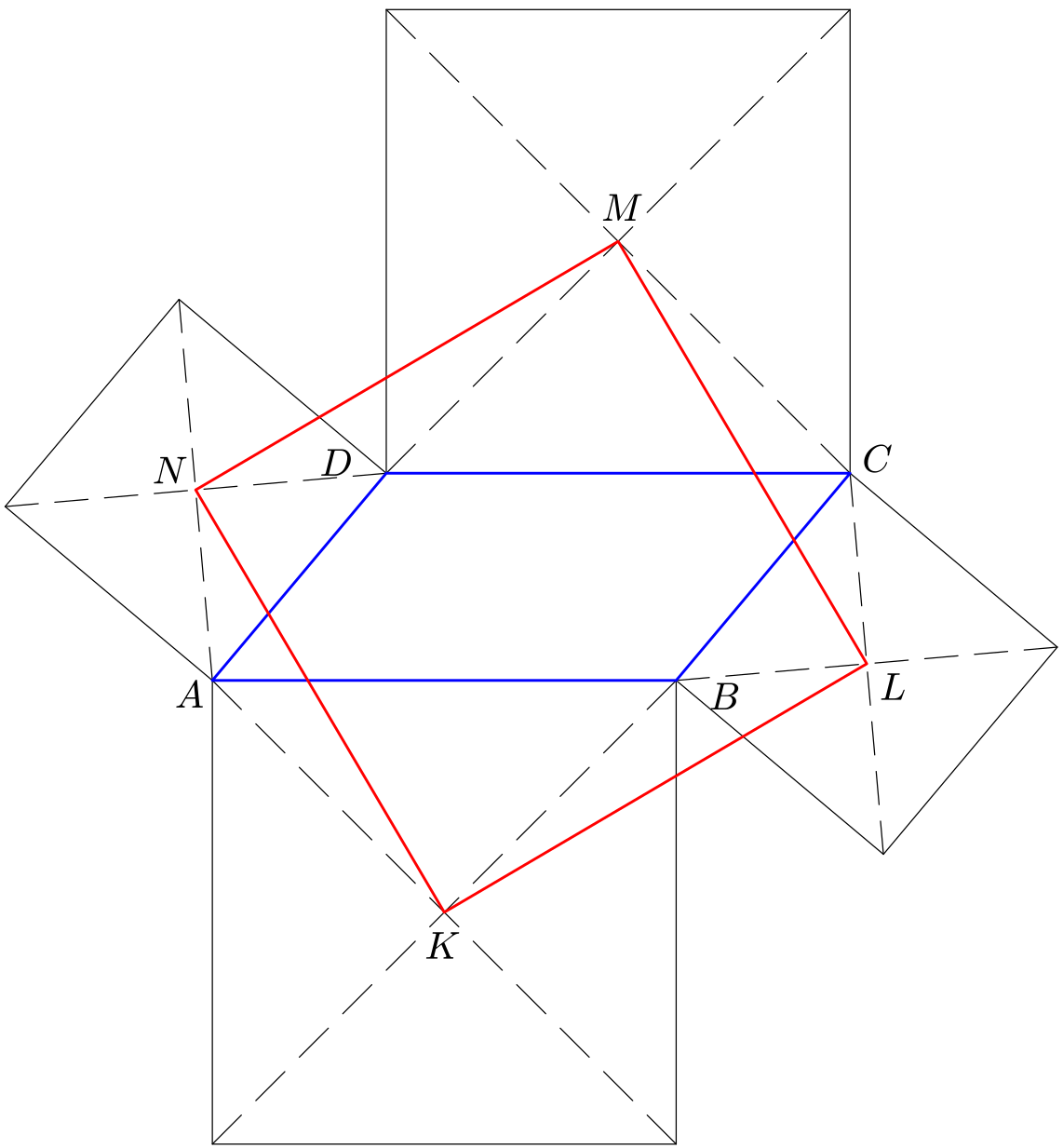
Rovnoběžník a čtverce
Ke každé straně rovnoběžníku
ABCD je sestrojen čtverec:
Dokažte, že středy těchto čtverců tvoří vrcholy dalšího čtverce a že se úhlopříčky rovnoběžníku
ABCD a čtverce
KLMN protínají v jediném bodě.
Řešení
Protože strany
AB a
CD mají stejnou délku, jsou čtverce nad těmito stranami shodné a platí
|DM|=|AK|. Obdobně zjistíme, že platí
|ND|=|NA|. Protože
ABCD je rovnoběžník, součet velikostí úhlů
DAB a
CDA je
180∘. Úhly
BAK,
NAD,
NDY a
XDM mají velikost
45∘. Z toho plyne, že součet velikostí úhlů
CDA a
YDX je
180∘, takže úhly
YDX a
DAB jsou shodné. Shodné jsou tedy i úhly
NAK a
NDM. Trojúhelníky
NDM a
NAK jsou tedy shodné a platí
|NM|=|NK|. Zopakujeme-li stejnou úvahu pro další strany čtyřúhelníku
KLMN, dostaneme
|NM|=|NK|=|KL|=|LM|. Čtyřúhelník
KLMN je tedy kosočtverec. Protože úhly
YDX a
DAB jsou shodné a úhly
MND,
KNA jsou také shodné, má úhel
MNK stejnou velikost jako úhel
DNA, tj.
90∘. Obdobnou úvahou zjistíme, že úhel
NLK je pravý. Čtyřúhelník
KLMN je tedy čtverec.
Označme O průsečík úhlopříček KM a BD. Protože jsou přínky AB, CD rovnoběžné, jsou úhly CDB, ABD shodné. Shodné jsou tedy i úhly MDO, KBO, a protože shodné jsou i úhly DOM a BOK a |DM|=|BK|, jsou trojúhelníky KBO, MDO shodné a bod O je středem úhlopříček KM a BD. Stejným bodem tedy musejí procházet i úhlopříčky LN a AC.