Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Kružnice a trojúhelník

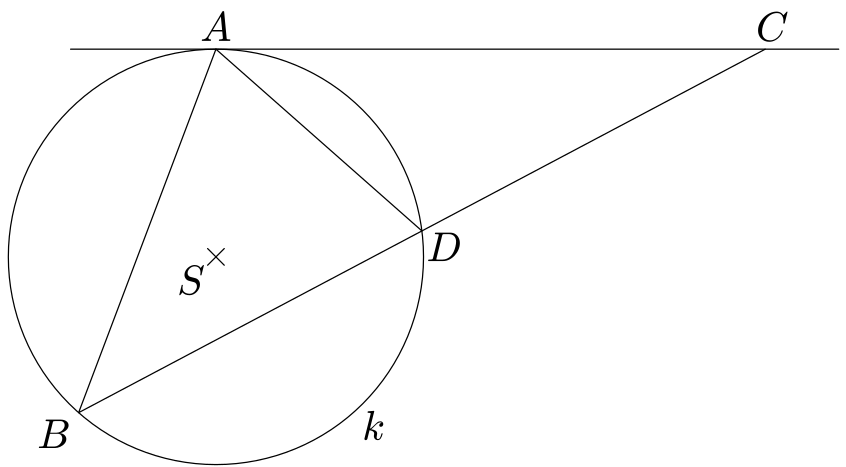
V rovině je dána kružnice $k$. Sestrojte trojúhelník $ABC$ těchto vlastností:

(1) Přímka $AC$ je tečnou kružníce $k$.
(2) Kružnice $k$ je opsána trojúhelníku $ABD$, kde $D$ je střed strany $BC$.
(3) Úsečka $AC$ je dvakrát delší než úsečka $AD$.

Řešení

Postup je založený na tom, že nejprve sestrojíme pomocný útvar, který je tomu výslednému geometricky podobný, a pak ho patřičně zvětšíme nebo zmenšíme. Úhel $CAD$ příslušný tětivě $AD$ se nazývá úsekový a má stejnou velikost jako obvodový úhel $ABD$ příslušný této tětivě. (Kdo si to nepamatuje ze školy a nedokže si to sám odvodit, může se podívat do brožurky S. Horáka Kružnice z edice Škola mladých matematiků).

Trojúhelníky $ACD$ a $BCA$ jsou tedy podobné a platí ${|AC|\over|CD|}={|BC|\over|AC|}={2|CD|\over|AC|}$, přičemž v poslední rovnosti jsme použili podmínku (2). Dostáváme $|CD|={1\over\sqrt2}|AC|={\sqrt2\over2}|AC|$ a podle (3) $|AD|={1\over2}|AC|$. Na tečně ke kružnici $k$ zvolíme bod $C_1$ a sestrojíme trojúhelník $AC_1D_1$ tak, že $|C_1D_1|={\sqrt2\over2}|AC_1|$ a $|AD_1|={1\over2}|AC_1|$. (Délka úsečky $|C_1D_1|$ je polovinou délky úhlopříčky ve čtverci o straně $AC_1$.)

Bod $B_1$ sestrojíme tak, aby bod $D_1$ byl středem úsečky $B_1C_1$. Hledané body $B$ a $D$ leží na průsečících přímek $AB_1$ a $AD_1$ s kružnicí $k$ a bod $C$ je průsečíkem přímek $BD$ a $AC_1$. Z podobnosti snadno ověříme, že trojúhelník $ABC$ a bod $D$ splňují podmínky (2) a (3).
Úloha byla zařazena do duhého kola 39. ročníku Matematické olympiády v kategorii B pro studenty středních škol.