Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Zajímavé vztahy v trojúhelníku
V trojúhelníku $ABC$ označme $D$ patu výšky na stranu $AB$ a na úsečce $DC$ zvolme bod $E$.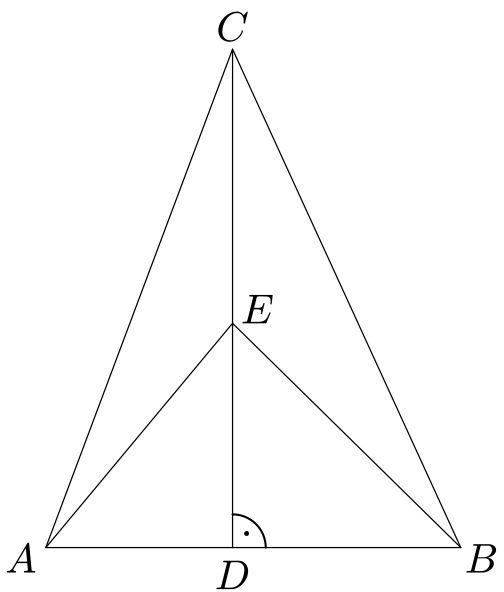
Jaký vztah platí, když bod $E$ leží na přímce $CD$ vně úsečky $CD$?
Řešení
Použijeme Pythagorovou větu. V pravoúhlých trojhúhelnících $ADC$, $ADE$ platí $|DC|^2=|AC|^2-|AD|^2=|BC|^2-|BD|^2$ a obdobně v trojúhelnících $DBC$, $DBE$ platí $|DE|^2=|AE|^2-|AD|^2=|BE|^2-|BD|^2$. Z obou rovnic vyjádříme $|AD|^2-|BD|^2$ a dostaneme $|AD|^2-|BD|^2=|AC|^2-|BC|^2=|AE|^2-|BE|^2$. Z poslední rovnosti již plyne dokazovaný vztah $|AC|^2-|AE|^2=|BC|^2-|BE|^2$.Jestliže bod $E$ leží na přímce $CD$ vně úsečky $CD$ na straně bodu $D$, pak obrázek vypadá takto:

Jestliže bod $E$ leží na přímce $CD$ vně úsečky $CD$ na straně bodu $C$, pak je situace podobná pprvnímu případu, jen body $C$ a $E$ si vymění role. Platí tedy vztah $|AE|^2-|AC|^2=|BE|^2-|BC|^2$, a tedy opět $|AC|^2-|AE|^2=|BC|^2-|BE|^2$.