Úlohy pro zábavu i pro poučení
Šikmá věž z cihel
Pro účel této úlohy si představme, že máme sadu cihel přesně stejné velikosti, hmotnosti a rovnoměrné hustoty. Položíme-li jednu cihlu na druhou, je jasné, jak daleko můžeme tu horní vysunout přes okraj té spodní, aniž by se překlopila a spadla: do poloviny. Těžiště horní cihly je pak přesně na hraně té spodní a nepřeklopí se.
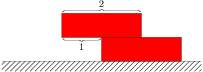
Trochu složitější je to se třemi cihlami. Je jasné, že v předchozí situaci už třetí cihlu před druhou předsunout nemůžeme; narušili bychom rovnováhu a obě by se překlopily. Musíme začít od začátku, či vlastně od konce. Třetí cihlu opět položíme tak, aby přečnívala přes druhou cihlu přesně jednou polovinou délky. Snadno zjistíme, že těžiště soustavy těchto dvou cihel je ve vzdálenosti $1\over2$ od přední hrany druhé cihly (pro zjednodušení uvažujeme cihly délky $2$, a protože cihly mají stejnou velikost, hmotnost a rovnoměrnou hustotu, můžeme velikost tíhové síly, kterou působí cihla, považovat rovněž za jednotkovou): hmotnost soustavy druhé a třetí cihly před těžištěm je $x+1+x$ a za těžištěm $2-x+1-x$. Musí tedy platit $x+1+x=2-x+1-x$, tj. $x={1\over2}$.
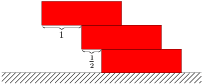
Můžeme tedy vysunout druhou a třetí cihlu společně přes okraj první cihly o $1\over2$, aniž by se celá věž zřítila. Přední okraj věže přečnívá hranu spodní cihly o $1+{1\over2}={3\over2}$.
Představme si, že máme k dispozici libovolný počet takových cihel. Jak až daleko může přední okraj takové šikmé věže přečnívat přes spodní cihlu, aniž by se zřítila?
Řešení
To je opět jedna z úloh, kde nás intuice může zradit. Už situace se třemi cihlami může vypadat trochu překvapivě, ale pořád ještě uvěřitelně, protože třetí cihla svou částí ještě leží nad tou první. Zkusme pokračovat, jak bylo naznačeno v zadání. Situace se čtyřmi cihlami vypadá následovně (pro účel dalšího pokračování upravíme označení):

Rovnice rovnováhy sil pro čtyři cihly vypadá takto: $(x_1+x_2+x_3)+(x_2+x_3)+x_3=(2-x_1-x_2-x_3)+(2-x_2-x_3)+(2-x_3)$, tj. $x_1+2x_2+3x_3=3$. Obdobným způsobem přepíšeme rovnici rovnováhy sil pro vrchní dvě cihly uvedenou v zadání úlohy: $x_1+2x_2=2$. Odečteme ji od předchozí rovnice a dostaneme $3x_3=1$, tj. $x_3={1\over3}$. Rovnovážný stav v případě čtyř cihel tedy nastane pro $x_1=1$, $x_2={1\over2}$, $x_3={1\over3}$. Postup snadno zobecníme matematickou indukcí. Rovnice rovnováhy pro $n$ cihel je $x_1+2x_2+\cdots+(n-1)x_{n-1}=n-1$ a pro $n+1$ cihel $x_1+ 2x_2+\cdots+(n-1)x_{n-1}+nx_n=n$, a z toho ihned plyne $x_n={1\over n}$. Postavíme-li tedy takto věž z $n+1$ cihel, cihla na vrchu věže bude přes spodní cihlu přečnívat o vzdálenost $a_n=x_1+x_2+x_3+\cdots +x_n=1+{1\over2}+{1\over3}+\cdots+{1\over n}$. To je částečný součet tzv. harmonické řady, která, jak známo, nekonverguje, tj. čísla $a_n$ tvoří rostoucí shora neomezenou posloupnost, matematický vyjádřeno $\lim_{n\to\infty}1+{1\over 2}+{1\over 3}+\cdots +{1\over n}=\infty$ (viz např.
https://cs.wikipedia.org/wiki/Harmonická_řada). Uvedeným způsobem stavěná šikmá věž tedy skutečně může svou základnu přesahovat libovolně daleko.


