Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Kouzelný čtverec
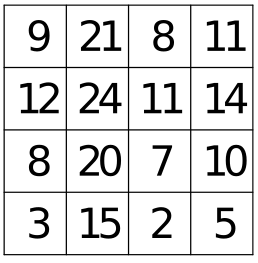
Ukážeme další kouzelnický trik, za kterým se skrývá jednoduchá matematika. Jardových slavil třicáté narozeniny. Protože o něm bylo známo, že se rád baví matematickými hádankami, jeden z hostů si vyžádal list papíru, nakreslil na něj následující čtvercovou mřížku a vyplnil ji čísly:
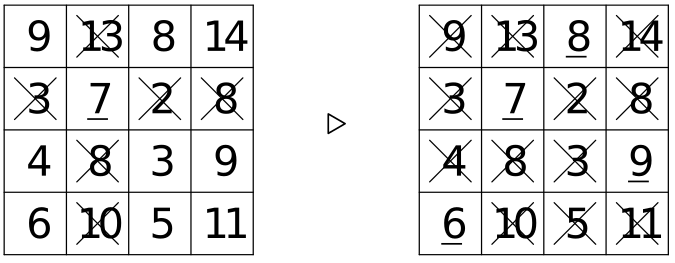
Předal mřížku Jardovi, otočil se k němu zády, aby na mřížku neviděl, a požádal ho, aby podtrhl jedno z čísel a vyškrtl všechna další čísla, která jsou ve stejném řádku a ve stejném sloupci – viz další obrázek vlevo, kde je vybráno číslo $7$ ve druhém řádku a druhém sloupci. V dalším kroku měl Jarda vybrat některé z čísel, které není podtrženo ani přeškrtnuto, podtrhnout je a opět vyškrtnout všechna další čísla, která jsou ve stejném řádku a ve stejném sloupci jako druhé podtržené číslo. Nakonec měl Jarda zopakovat postup ještě jednou a nakonec podtrhnout zbylé číslo. Mohlo to vypadat např. jako obrázku vpravo:
Kamarád pak Jardovi řekl, ať sečte čtyři podtržená čísla a poblahopřál mu k narozeninám vyjádřených tímto součtem. Jak to dokázal?
Řešení
Trik je velmi jednoduchý, i když nemusí být zcela snadné na něj přijít. Jardův kamarád rozložil číslo $30$ na součet osmi čísel a připravil si pracovní verzi mřížky tak, že vlevo od každého řádku a nad každý sloupec napsal jedno z těch osmi čísel. V příkladu uvedeném v úloze to byla čísla $7$, $1$, $2$, $4$, $2$, $6$, $1$, $7$ vyznačená červeně.
Pak mřížku vyplnil tak, že do každé buňky vepsal součet čísla před příslušným řádkem a na příslušným sloupcem. Způsob postupného výběru podtržených čísel zajistí, že na každém řádku a v každém sloupci je právě jedno z nich. To znamená, že do součtu podtržených čísel vstupuje každé z čísel vlevo od řádků a nad sloupci právě jednou. V našem případě $8+7+9+6=(7+1)+(1+6)+(2+7)+(4+2)=30$. Stejný trik lze použít pro libovolně velkou čtvercovou mřížku, která má alespoň tři řádky a tři sloupce.