Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Kruhová deska
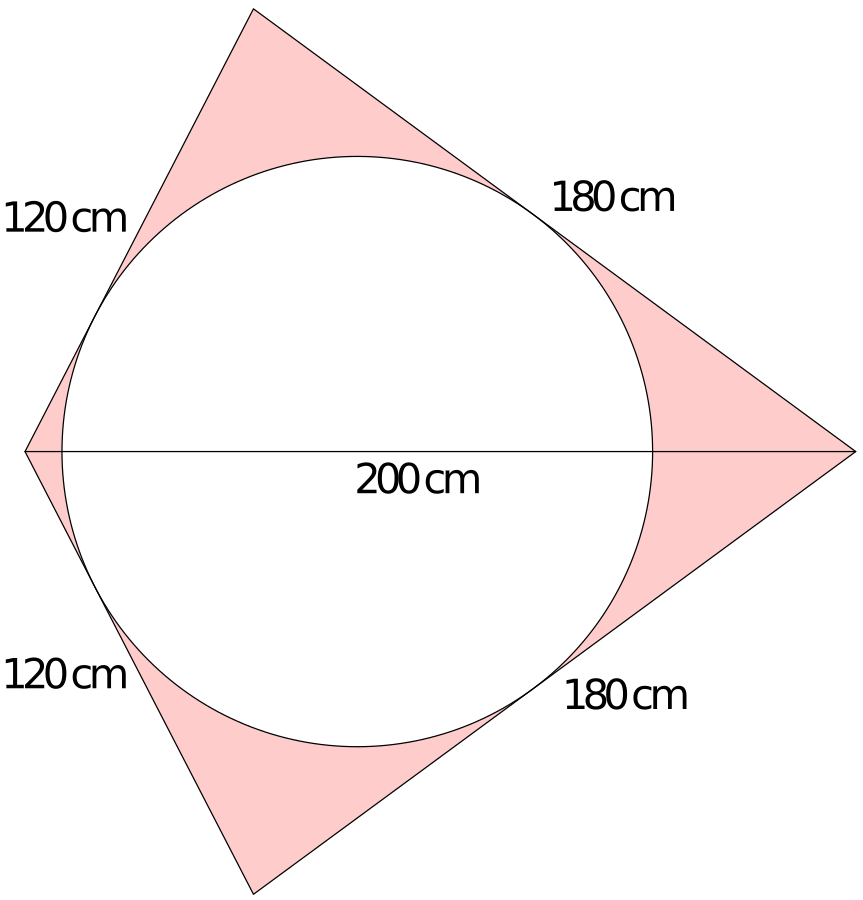
Truhlář má k dispozici desku ve tvaru čtyřúhelníku, jehož dvě sousední strany mají délku 120 cm, druhé dvě sousední strany mají délku 180 cm a větší úhlopříčka má délku 200 cm. Chce z ní vyříznout co největší kruhovou desku na stůl. Kde bude střed kruhové desky a jaký bude její průměr?
Řešení
Označme vrcholy čtyřúhelníkové desky $A$, $B$, $C$, $D$ a délky stran $|AB|=|AD|=a$, $|CB|=|CD|=b$, $|AC|=c$. Úkolem je najít střed $S$ a velikost $r$ poloměru kružnice vepsané čtyřúhelníku $ABCD$.

Protože trojúhelníky $ABC$, $ADC$ jsou shodné, úhly $DAC$ a $CAB$ mají stejnou velikost a přímka $AC$ je osou úhlu $DAB$. Střed $S$ kružnice vepsané čtyřúhelníku $ABCD$ tedy leží na úsečce $AC$. Označme $x$ jeho vzdálenost od bodu $A$. Označme $E$, $F$ body dotyku vepsané kružnice se stranami $AD$, $CD$.
Pravoúhlé trojúhelníky $SDE$, $SDF$ jsou shodné, jejich úhly při vrcholu $D$ tedy mají stejnou velikost $\alpha$. Označíme-li $\beta$, $\gamma$ velikosti úhlů $ASD$, $DSC$, platí $\gamma=180^\circ-\beta$. Podle sinové věty v trojúhelnících $ASD$, $SCD$ platí ${a\over x}={\sin\beta\over\sin\alpha}$ a ${b\over c-x}={\sin\gamma\over\sin\alpha}$, a protože $\sin\gamma=\sin(180^\circ-\beta)=\sin\beta$, dostáváme ${a\over x}={b\over c-x}$. Odtud vypočteme $x={ac\over a+b}$. Po dosazení daných rozměrů desky dostáváme $x=80$ cm.
Velikost průměru kružnice zjistíme porovnáním obsahů trojúhelníků $ASD$, $SCD$, $ACD$. Úsečka $SE$ je výškou trojúhelníku $ASD$ na stranu $AD$, obsah tohoto trojúhelníku je tedy roven ${1\over2}ar$. Obdobně obsah trojúhelníku $SCD$ je roven ${1\over2}br$. Pro výpočet obsahu trojúhelníku $ACD$ máme k dispozici jen délky jeho tří stran. Jeho obsah vypočteme pomocí
Heronova vzorce: $\sqrt{{o\over2}({o\over2}-a)({o\over2}-b)({o\over2}-c)}$, kde $o=a+b+c$ je velikost obvodu trojúhelníku $ACD$. Po dosazení daných veličin vypočteme $r\approx 71{,}1$ cm. Průměr desky bude přibližně $142{,}2$ cm.