Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Archimedova kruhová dvojčata
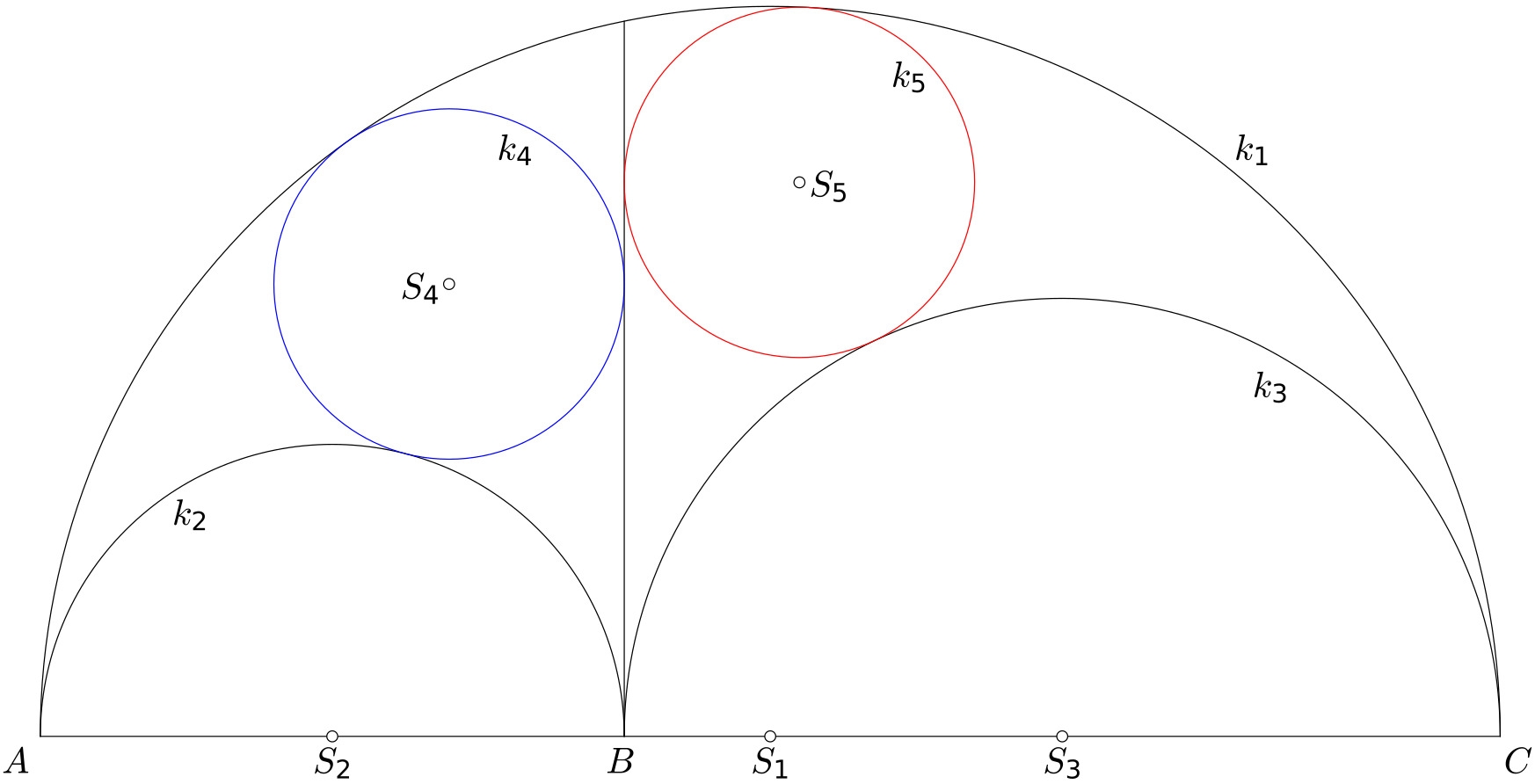
Je dána půlkružnice $k_1$ o poloměru $r_1$ a v ní dvě půlkružnice $k_2$, $k_3$ se středy ležícími na průměru půlkružnice $k_1$ a s poloměry $r_2$, $r_3$, jejichž součet se rovná $r_1$.
Plocha mezi půlkružnicemi $k_1$, $k_2$, $k_3$ se nazývá arbelos (z řeckého arbylos, ševcovský nůž). V bodě dotyku půlkružníc $k_2$, $k_3$ je vztyčena kolmice k průměru, která dělí arbelos na dvě části. V každé z nich je sestrojena kružnice $k_4$, $k_5$, která se dotýká kolmice a půlkružníc $k_1$, $k_2$, resp. $k_1$, $k_3$. Dokažte, že kružnice $k_4$, $k_5$ jsou shodné.
Úloha pochází z Archimedovy "Knihy lemat", která se dochovala v překladu, jejž pořídil arabský matematik a astronom Thabit Qurra ibn al-Ḥarrānī.
Řešení
Ze středů $S_4$, $S_5$ kružnic $k_4$, $k_5$ spustíme kolmice $S_4D$, $S_5E$ na průměr půlkružnice $k_1$ a jejich délky označíme $h_1$, $h_2$.
Půlkružnice $k_1$ a kružnice $k_4$ mají v bodě dotyku společnou tečnu, spojnice bodu dotyku se středem $S_1$ půlkružnice $k_1$ proto prochází středem $S_4$ kružnice $k_4$. Protože $|S_2D|=r_2-r_4$, podle Pythagorovy věty pro pravoúhlý trojúhelník $S_2DS_4$ platí $h_1^2+(r_2-r_4)^2=(r_2+r_4)^2$. Po úpravě dostaneme $h_1^2=4r_2r_4$. Podobně pro trojúhelník $DS_1S_4$ platí $h_1^2+(r_1-2r_2+r_4)^2=(r_1-r_4)^2$, tj. $h_1^2=4(r_1r_2+r_2r_4-r_1r_4-r_2^2)$. Srovnáním obou výrazů pro $h_1^2$ a využitím vztahu $r_1=r_2+r_3$ dostaneme $r_4={r_2\cdot r_3\over r_2+r_3}$. Obdobným postupem pro trojúhelníky $ES_3S_5$ a $S_1ES_5$ vypočteme $r_5={r_2\cdot r_3\over r_2+r_3}$. Tedy skutečně $r_4=r_5$ a kružnice $k_4$, $k_5$ jsou shodné.