Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Rozklad čtverce

Ve čtverci o straně délky $1$ jsou z každého vrcholu vepsány čtvrtkružnice o poloměru $1$. Čtverec je tím rozdělen na $9$ částí.

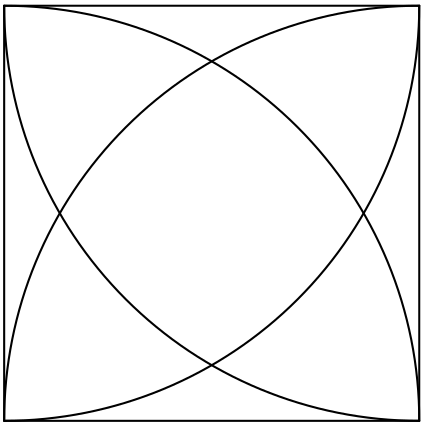
Vypočtěte velikosti obsahů těchto částí.
Tato úloha byla zařazena do přípravného kola 30. ročníku Matematické olympiády v kategorii C pro studenty středních škol.

Řešení

Čtverec je rozdělen na tři druhy částí, z nichž dvě čteřice jsou vždy shodné. Velikosti jejich obsah; označíme $x$, $y$, $z$.

Pro celý čtverec platí $$x+4y+4z=1.$$ Pro čtvrtkruh platí $$x+3y+2z={\pi\over4}.$$ Pro sjednocení dvou kruhových výsečí, jejichž průnikem je rovnostranný trojúhelník $ABK$, platí $$x+2y+z={\pi\over3}-{\sqrt3\over4}$$ (dvakrát kruhová výseč, která je šestinou celého kruhu, mínus obsah trojúhelníku $ABK$).

Odečteme-li druhou rovnici od první a třetí od druhé, dostaneme $$\eqalign{y+2z&=1-{\pi\over4}\cr y+z&={\pi\over4}-{\pi\over3}+{\sqrt3\over4}\cr}$$ a odtud $$z=1-{\pi\over6}-{\sqrt3\over4},\ y=-1+{\pi\over12}+{\sqrt3\over2},\ x=1+{\pi\over3}-\sqrt3.$$