Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Je každý trojúhelník rovnoramenný?

Péťa, kterého baví objevovat matematiku, se zase jednou ukvapil (viz úlohu Kružnice se dvěma středy) a přišel s důkazem, že každý trojúhelník je rovnoramenný. Nakreslil následující obrázek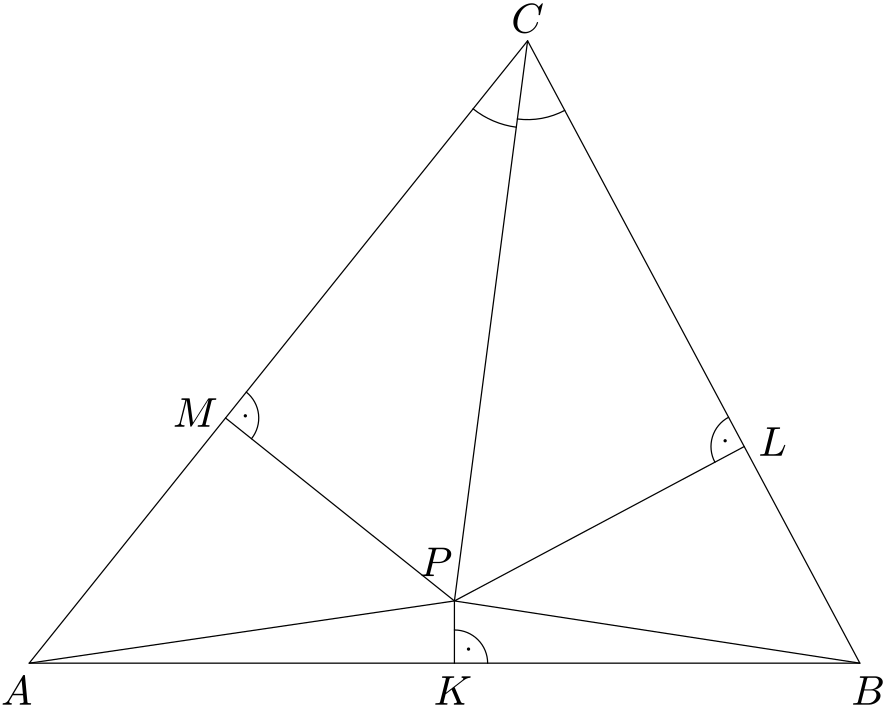

a provedl následující úvahu: V trojúhelníku $ABC$ sestrojíme osu strany $AB$ a osu úhlu při vrcholu $C$. Jejich průsečík označíme $P$. Z bodu $P$ spustíme kolmice k přímkám $BC$ a $AC$. Protože bod $P$ leží na ose úhlu $BCA$, má stejnou vzdálenost od přímek $AC$, $BC$, tj. $|PL|=|PM|$, a úhly $LCP$, $PCM$ jsou shodné, takže také $|LC|=|MC|$. Protože bod $P$ leží na ose strany $AB$, má stejnou vzdálenost od bodů $A$, $B$, tj. $|PA|=|PB|$, a tedy také $|LB|=|MA|$. Dostáváme $|AC|=|AM|+|MC|=|LC|+|BL|=|BC|$, takže trojúhelník $ABC$ musí být rovnoramenný. Kde udělal Péťa chybu?

Řešení

Chyba je opět v náčrtku řešení. Péťa se snažil zachytit obecnou situaci tak, že osa úhlu $BCA$ a osa strany $AB$ mají společný bod uvnitř trojúhelníku $ABC$, což platí právě jen v případě rovnoramenného trojúhelníku, kdy obě osy splývají. Při přesné konstrukci v situaci, kterou Péťa načrtl, obrázek vypadá takto:

Při řešení konstrukčních geometrických úloh je třeba dbát na to, abychom se nevhodným náčrtkem nenechali svést k chybné úvaze.