Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Kružnice se dvěma středy

Péťu matematika baví, ale občas se ukvapí. Onehdá se přihlásil s objevem, že kružnice může mít dva různé středy. Nakreslil následující obrázek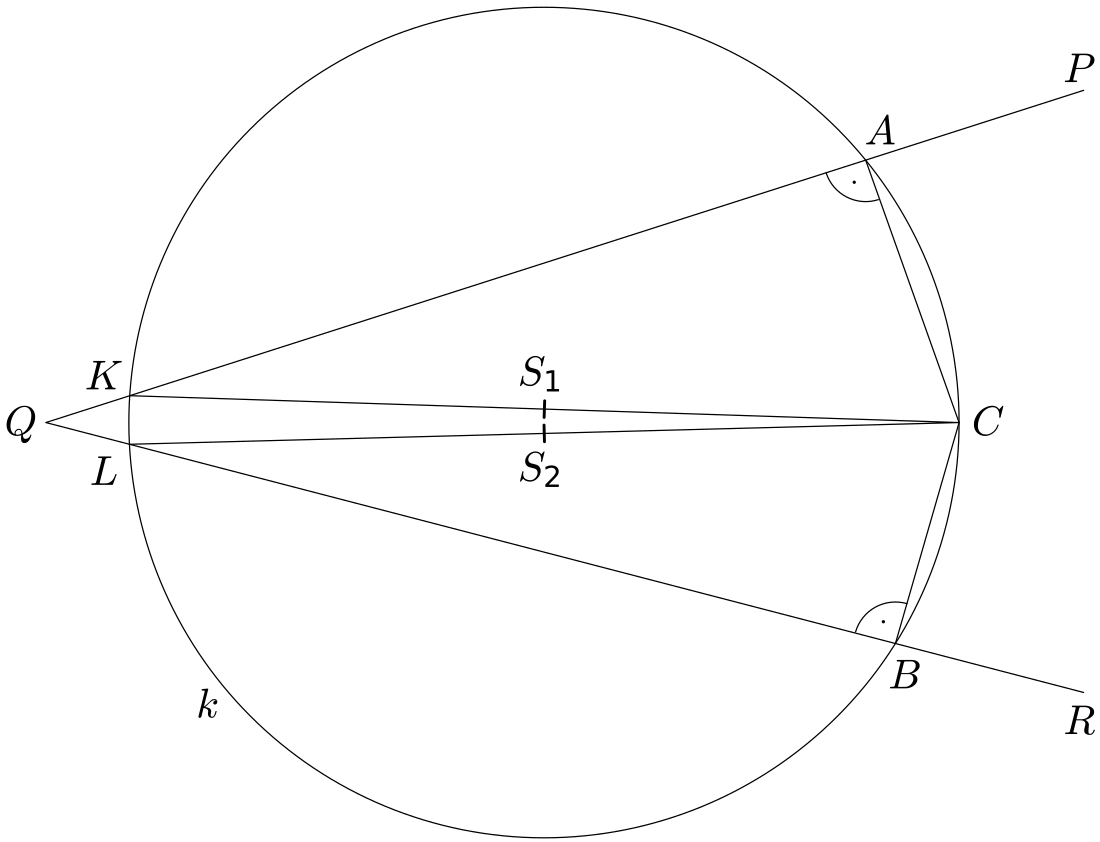

a vysvětlil, jak na to přišel: Narýsujeme úhel

$PQR$ a na jeho ramenech zvolíme body

$A$ a

$B$ . Z bodu

$A$ vedeme kolmici k přímce

$QP$ a z bodu

$B$ vedeme kolmici k přímce

$QR$ . Průsečík obou kolmic označíme

$C$ . Sestrojíme kružnici

$k$ procházející body

$A$ ,

$B$ a

$C$ a další průsečíky kružnice

$k$ s přímkami

$QP$ ,

$QR$ označíme

$K$ ,

$L$ . Podle Thaletovy věty přepony pravoúhlých trojúhelníků

$KCA$ a

$LCB$ musí být průměry kružnice

$k$ . Středy úseček

$KC$ a

$LC$ jsou tedy středy kružnice

$k$ . Kde udělal Péťa chybu?

Řešení

Chyba je v náčrtku řešení. Péťa se snažil zachytit obecnou situaci tak, že kružnice

$k$ protne přímky

$QP$ ,

$QR$ v dalších dvou bodech, a poté na tento náčrtek aplikoval Thaletovu větu. Neuvědomil si, ža právě podle Thaletovy věty musí kružnice

$k$ procházet bodem

$Q$ . Oba průměry na Péťově náčrtku pak splynou, a tak splynou i oba zdánlivě různé středy

$S_1$ a

$S_2$ .
Při řešení konstrukčních geometrických úloh je třeba dbát na to, abychom se nevhodným náčrtkem nenechali svést k chybné úvaze.