Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Čtyři kružnice v trojúhelníku

Je dán obecný trojúhelník $ABC$. K jemu vepsané kružnici jsou vedeny tři tečny rovnoběžné se stranami trojúhelníku. Tečny v trojúhelníku vytínají tři menší trojúhelníky, do nichž jsou opět vepsány kružnice.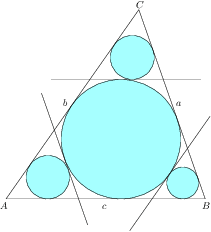

Úkolem je vyjádřit součet obsahů všech čtyř kruhů ohraničených těmito kružnicemi pomocí délek stran $a$, $b$, $c$ trojúhelníku $ABC$.

Řešení

Označme $A_1$, $B_1$ průsečíky stran $AC$, $BC$ s tečnou kružnice vepsané trojúhelníku $ABC$ rovnoběžnou se stranou $AB$.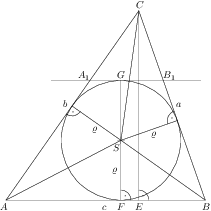

Trojúhelníky $ABC$ a $A_1B_1C$ jsou podobné. Koeficient podobnosti se rovná podílu velikostí výšek obou trojúhelníků: ${v-2\varrho\over v}=1-{2\varrho\over v}$, kde $v=|EC|$ je výška trojúhelníku $ABC$ ke straně $AB$ a $\varrho$ je poloměr kružnive vepsané trojúhelníku $ABC$. Ve stejném poměru jsou i délky stran $|A_1B_1|$ a $c=|AB|$ obou trojúhelníků a velikosti poloměrů jim vepsaných kružnic. Obsah trojúhelníku $ABC$ lze vyjádřit jednak pomocí délky strany $c$ a výšky $v$, jednak jako součet obsahů trojúhelníků $ABS$, $BCS$ a $CAS$: $P={1\over2}cv={1\over2}(a+b+c)\varrho=s\varrho$, kde $s$ označuje poloviční obvod trojúhelníku $ABC$. Z toho plyne ${2\varrho\over v}={c\over s}$, a tedy koeficient podobnosti trojúhelníků $A_1B_1C$, $ABC$ je roven $1-{c\over s}$. Kruh vepsaný trojúhelníku $ABC$ má obsah $Q=\pi\varrho^2$ a kruh vepsaný trojúhelníku $A_1B_1C$ má obsah $\pi\left[\left(1-{c\over s}\right)\varrho\right]^2=\left(1-{c\over s}\right)^2Q$.
Úvahu můžeme zopakovat pro každý ze dvou zbývajících trojúhelníků vyťatých tečnami kružnice vepsané trojúhelníku $ABC$ rovnoběžnými se stranami $BC$ a $AC$ a zjistíme, že součet obsahů všech čtyř kruhů se rovná $Q+\left(1-{a\over s}\right)^2Q+\left(1-{b\over s}\right)^2Q+\left(1-{c\over s}\right)^2Q=Q{s^2+(s-a)^2+(s-b)^2+(s-c)^2\over s^2}$. Upravíme čitatel $s^2+(s-a)^2+(s-b)^2+(s-c)^2=4s^2-2as-2bs-2cs+a^2+b^2+c^2=4s^2-2s(a+b+c)+a^2+b^2+c^2=4s^2-2s2s+a^2+b^2+c^2=a^2+b^2+c^2$ a obsah $Q$ vyjádříme pomocí výše uvedeného vztahu jako $Q=\pi\varrho^2=\pi\left({P\over s}\right)^2=\pi{(s-a)(s-b)(s-c)\over s}$, kde jsme pro vyjádření obsahu obsahu trojúhelníku $ABC$ použili Heronův vzorec $P=\sqrt{s(s-a)(s-b)(s-c)}$. Součet obsahů všech čtyř kruhů je tedy roven $\pi{(s-a)(s-b)(s-c)(a^2+b^2+c^2)\over s^3}={(b+c-a)(a+c-b)(a+b-c)(a^2+b^2+c^2)\over(a+b+c)^3}$.
Úloha byla zařazena do domácího kola pro kategorii B v 35. ročníku Matematické olympiády konané ve školním roce 1985/86.