Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Trojúhelník s nejmenším obvodem

Je dán ostroúhlý trojúhelník

$ABC$ a uvnitř jeho strany

$AB$ bod

$K$ . Najděte uvnitř strany

$BC$ bod

$L$ a uvnitř strany

$AC$ bod

$M$ tak, aby obvod trojúhelníku

$KLM$ byl minimální.

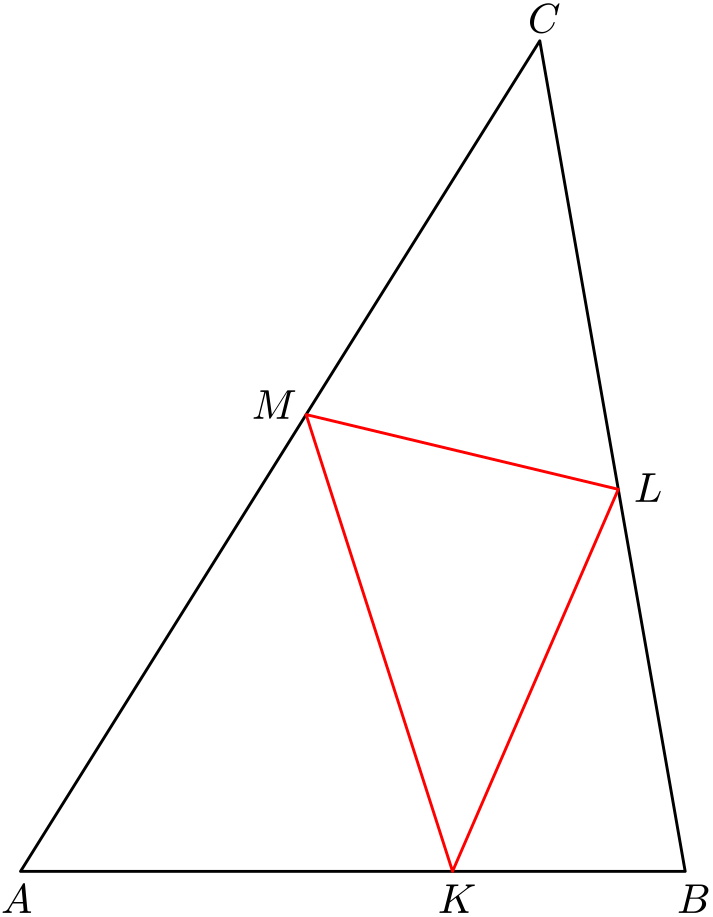
Tato úloha byla zařazena do přípravného kola 30. ročníku Matematické olympiády v kategorii C pro studenty středních škol.

Řešení

Úlohu vyřešíme vtipnou geometrickou úvahou. Sestrojíme bod

$K_1$ souměrně sdružený k bodu

$K$ podle strany

$BC$ a bod

$K_2$ souměrně sdružený k bodu

$K$ podle strany

$AC$ . Platí

$|KL|=|K_1L|$ ,

$|KM|=|K_2M|$ , takže obvod trojúhelníku

$KLM$ je roven délce lomené čáry

$K_1LMK_2$ .

Ta bude nejmenší, budou-li body

$L$ ,

$M$ ležet na přímce

$K_1K_2$ .

Protože je trojúhelník

$ABC$ ostroúhlý, snadnou úvahou o velikostech úhlů

$CKK_1$ ,

$K_2KC$ a

$K_2CK_1$ ověříme, že průsečíky přímky

$K_1K_2$ s přímkami

$BC$ ,

$AC$ jsou vnitřními body úseček

$BC$ ,

$AC$ .