Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Velká a malá ručička na hodinách

Starší řidiči si jistě pamatují poučku z autoškoly, že při řízení mají být ruce na volantu v poloze "za deset minut dvě" nebo "deset deset". U dnešních menších volantů s posilovačem řízení se za optimální z hlediska bezpečnosti považuje poloha "tři čtvrtě na tři". To jsou ovšem jen symbolické, přibližné instrukce. Podle nich by totiž obě ruce nebyly ve stejné výšce. Existuje vůbec postavení hodinových ručiček symetrické podle svislé osy? Jaký čas v takovém okamžiku hodiny ukazují? Předpokládejme, že ručičky neposkakují, pohybují se rovnoměrným pohybem.

Řešení

Každou hodinu proběhne velká ručička celých $360^\circ$, zatímco malá ručička proběhne jen úsek $30^\circ$ mezi dvěma sousedními označeními hodin. Symetrické postavení obou ručiček bychom tedy měli hledat v průběhu každé hodiny. Označíme $n$ počet celých hodin, které dosud uběhly, a část další hodiny, která uplynula, označíme $x$, $0\le x<1$. Nejprve uvažujme situaci, kdy je malá ručička v pravé polovině ciferníku, tj. $0\le n < 6$.

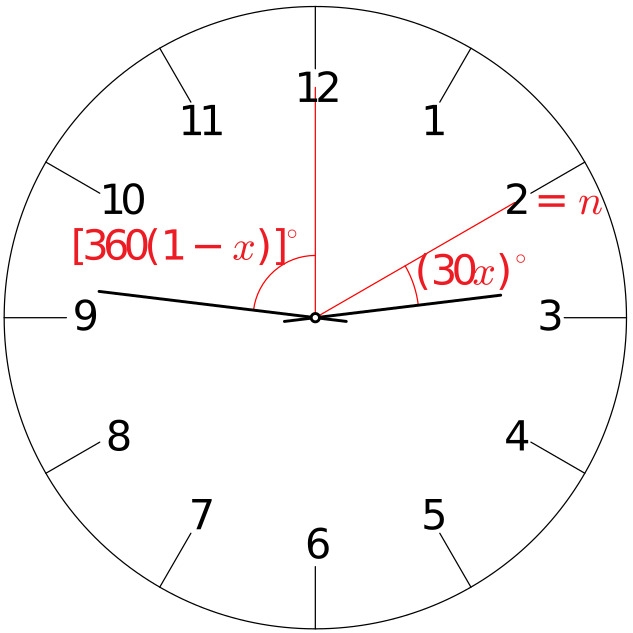
Úhel, který svírá malá ručička se spojnicí středu a dvanáctkou na ciferníku, má velikost $[30(n+x)]^\circ$. Velká ručička mezitím v dané hodině proběhla úhel $(360x)^\circ$ a se spojnicí středu a dvanáctkou na ciferníku svírá úhel velikosti $(360-360x)^\circ=[360(1-x)]^\circ$. Obě ručičky jsou v symetrické poloze, když $30(n+x)=360(1-x)$, tj. když $x={12-n\over13}$.
V případě, že je malá ručička v levé polovině ciferníku, tj. $6\le n\le12$, svírá se spojnicí středu a dvanáctkou na ciferníku úhel velikosti $[360-30(n+x)]^\circ$, zatímco velká ručička úhel $(360x)^\circ$.

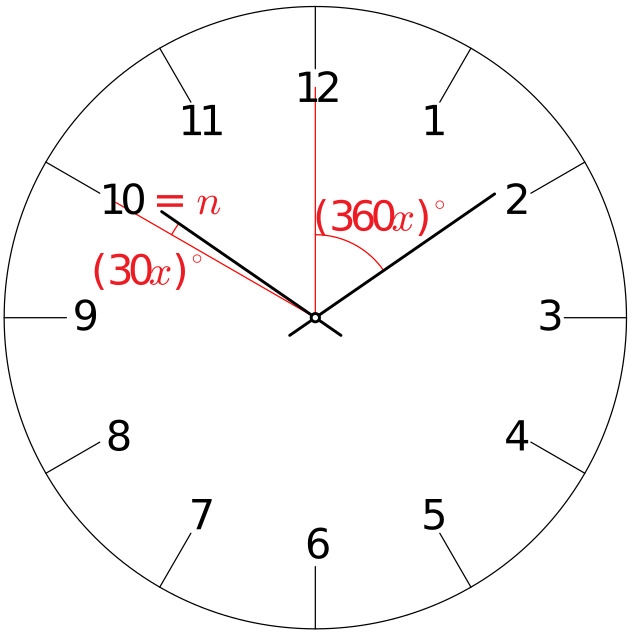
Obě ručičky jsou v symetrické poloze, když $360-30(n+x)=360x$, odkud opět dostáváme $x={12-n\over13}$.
Pro každé $n=0,1,2,\dots,12$ tedy dostáváme jedno řešení úlohy odpovídající času $x={12-n\over13}$ hodin. Konkrétně poloze "tři čtvrtě na tři" odpovídá čas $2+{10\over13}$ hodin, tj. přibližně 2h 46' 09", a poloze "deset deset" odpovídá čas $10+{2\over13}$ hodin, tj. přibližně 10h 9' 14".