Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Vyřezávání kruhů

Truhláři zbyla kruhová deska o poloměru 1 m. Chtěl by z ní vyříznout tři nebo čtyři menší stejně velké kruhové desky na stoličky tak, aby odpad byl co nejmenší.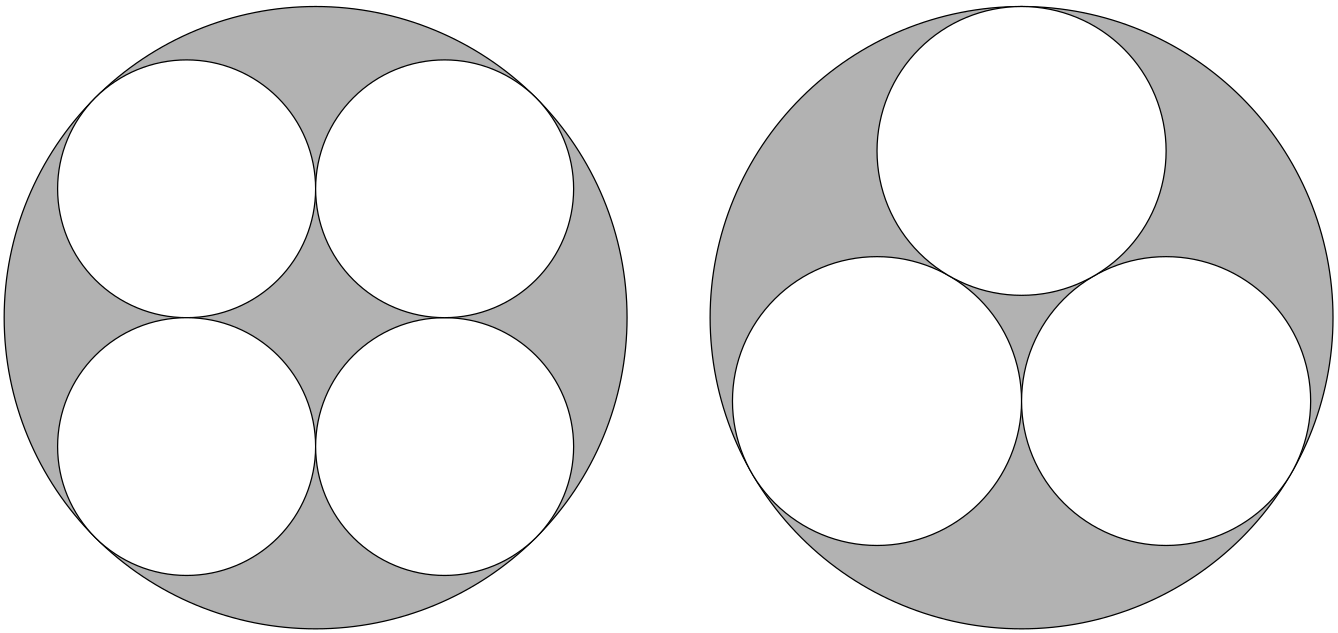

Jak velký poloměr by měla mít každá ze čtyř desek a jak velký poloměr by měla mít každá ze tří desek? V kterém případě bude odpad menší?

Řešení

Označme $r=1$ poloměr zpracovávané kruhové desky (pro zjednodušení zápisu budeme při výpočtu vynechávat délkové jednotky). Nejprve prozkoumáme případ čtyř menších desek, jejich poloměr označíme $r_1$.

Délka poloměru $r$ je rovna součtu délky poloměru $r_1$ a poloviny délky úhlopříčky ve čtverci $ABCD$. Jeho strana má délku $2r_1$, polovina délky jeho úhlopříčky je tedy $\sqrt2 r_1$ a $r=r_1(1+\sqrt2)$. Odtud $r_1={1\over\sqrt2+1}r=(\sqrt2-1)r\approx 0{,}414$. (V poslední rovnosti jsme využili známého vztahu $a^2-b^2=(a+b)(a-b)$.) Obsah menší kruhové desky je $P_1=\pi r_1^2=\pi (\sqrt2-1)^2r^2$ a všechny čtyři desky mají obsah $4P_1=\pi (\sqrt2-1)^2r^2\approx0{,}686\pi r^2$.

Obdobně postupujeme v případě tří menších desek. Označme jejich poloměr $r_2$. Pak délka poloměru $r$ je rovna součtu délky poloměru $r_2$ a dvou třetin délky výšky rovnostranného trojúhelníku $ABC$. (Výšky v rovnostranném trojúhelníku splývají s těžnicemi a protínají se v těžišti, které leží ve dvou třetinách délky těžnice od vrcholu.)

Jeho strana má délku $2r_2$ a (například podle Pythagorovy věty) jeho výška má délku $\sqrt3 r_2$. Platí tedy $r=({2\over3}\sqrt3+1)r_2$. Odtud $r_2={3\over 2\sqrt3+3}r=(2\sqrt3-3)r\approx0{,}464$. Obsah menší kruhové desky v tomto případě je $P_2=\pi r_2^2=\pi(2\sqrt3-3)^2r^2\approx0{,}646\pi r^2$ a všechny tři desky mají obsah $3P_2=3\pi(2\sqrt3-3)^2r^2\approx0{,}646\pi r^2$.

Odpad bude o něco menší v případě čtyř vyříznutých desek.