Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Rovnoběžník a rovnostranné trojúhelníky

Na obrázku je rovnoběžník $ABCD$, k jehož stranám $AB$, $AD$ přiléhají rovnostranné trojúhelníky $AEB$, $ADF$.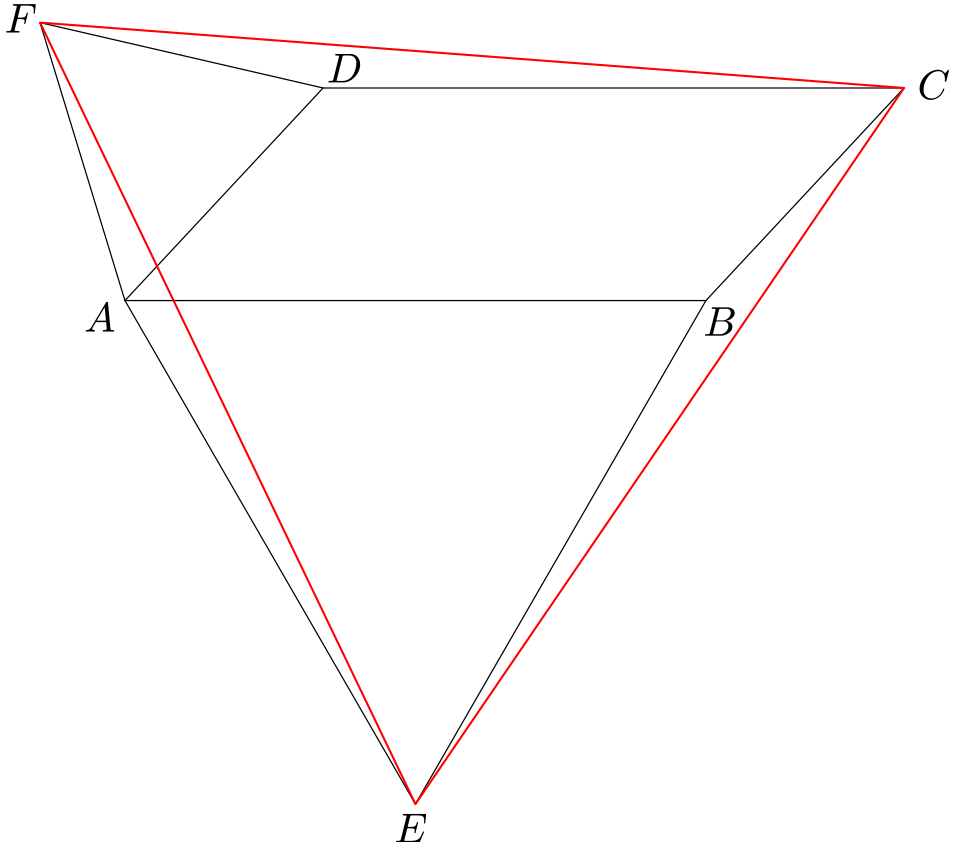

Zkuste dokázat, že trojúhelník $ECF$ je také rovnostranný.

Řešení

Vzhledem k tomu, že $|AE|=|BE|=|DC|$ a $|AF|=|BC|=|DF|$, je trojúhelník $ECF$ rovnostranný, právě když jsou všechny tři trojúhelníky $AEF$, $BEC$, $DCF$ shodné. K tomu stačí ukázat, že úhly v těchto trojúhelnících při vrcholech $A$, $B$, $D$ jsou stejně velké.

Pro úhly při vrcholech $B$ a $D$ to je ihned vidět z toho, že protější úhly $\alpha$ v rovnoběžníku jsou stejně velké a všechny úhly v rovnostranných trojúhelnících mají velikost $60^\circ$. Úhly při vrcholech $B$ a $D$ v trojúhelnících $BEC$, $DCF$ tedy mají velkost $360^\circ-\alpha-60^\circ=300^\circ-\alpha$. Velikost úhlu v trojúhelníku $AEF$ při vrcholu $A$ je rovna $60^\circ+\beta+60^\circ=60^\circ+(180^\circ-\alpha)+60^\circ=300^\circ-\alpha$.