Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Koule a krychle
Je dána krychle $ABCDEFGH$ o hraně délky $a$. Určete střed a délku poloměru $r$ kulové plochy, která protíná stěnu $BCG$ v kružnici $k$ vepsané čtverci $BCGF$ a prochází středem $P$ strany $AB$.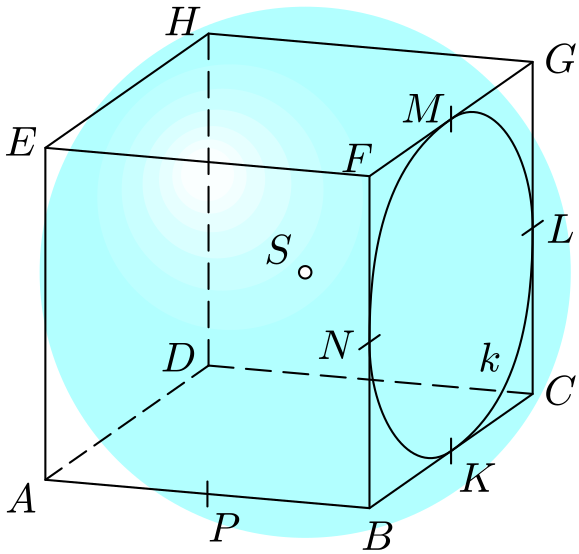
Řešení
Střed $S$ kulové plochy leží na kolmici vedené středem $O_1$ čtverce $BCGF$ a kolmé k jeho rovině, tedy na spojnici bodu $O_1$ a středu $O_2$ čtverce $ADHE$. Poloha středu $S$ bude určena, jestliže vypočteme jeho vzdálenost $x$ od bodu $O_1$. Označme $Q$ střed krychle.