Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Obsah mezikruží
Na obrázku je vybarveno mezikruží vytvořené dvěma soustřednými kružnicemi. Červeně vyznačená úsečka je nejdelší tětivou větší kružnice dotýkající se menší kružnice (je to samozřejmě jedna z nekonečně tětiv těchto vlastností). Tětiva má délku $t$.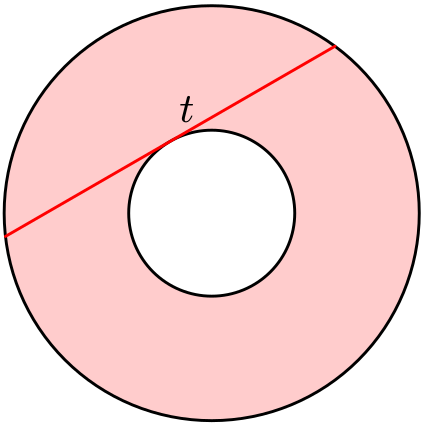
Řešení
Na první pohled se může zdát, že jediný údaj – délka $t$ tětivy – je pro určení plošného obsahu mezikruží málo. Další potřebná informace je však v tom, že je to tětiva dotýkající se vnitřní kružnice. Označme $r$ poloměr vnitřní kružnice a $R$ poloměr vnější kruznice. Obsah mezikruží je rozdílem obsahů kruhů daných vnější a vnitřní kružnicí: $P=\pi R^2-\pi r^2=\pi(R^2-r^2)$. Z Pythagorovy věty plyne $R^2-r^2=({t\over2})^2$. Z obou vztahů dostáváme $P=\pi ({t\over2})^2$. Velikost obsahu mezikruží se tedy rovná velikosti obsahu kruhu o průměru $t$.