Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Kolmé tětivy

V kružnici jsou dány dvě tětivy $AC$, $BD$, které se protínají pod pravým úhlem v bodě $F$. Bod $E$ je patou výšky v trojúhelníku $AFD$ spuštěné z bodu $F$. Bod $G$ je průsečíkem přímek $BC$, $EF$. Dokažte, že bod $G$ je středem úsečky $BC$.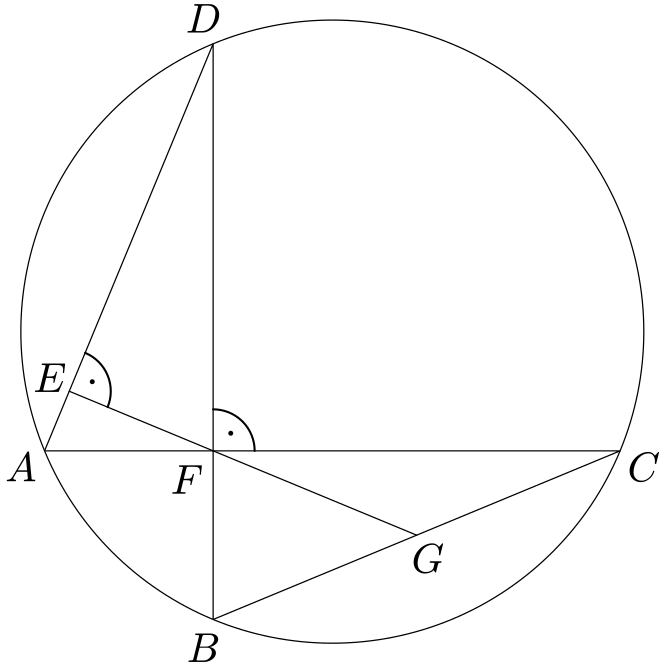

Řešení

V pravoúhlých trojúhelnících $FDE$, $AFE$ platí $\alpha+\beta=\beta+\gamma=\gamma+\delta=90^\circ$.

Odtud dostáváme $\gamma=\alpha$ a $\delta=\beta$. Protože úhly $BDA$ a $BCA$ jsou obvodové úhly nad tětivou $AB$, jsou shodné, tj. $\phi=\gamma=\alpha$. Shodné jsou i obvodové úhly nad tětivou $CD$, tj. $\psi=\delta=\beta$. Trojúhelníky $CFG$ a $BGF$ jsou tedy rovnoramenné, a proto platí $|BG|=|FG|=|CG|$.