Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Lichoběžník a kružnice
Délky základen rovnoramenného lichoběžníku $ABCD$ jsou v poměru $|AB|:|CD|=3:2$. Kružnice sestrojená nad průměrem $AB$ protíná základnu $CD$ tak, že její část ležící uvnitř kružnice má délku ${1\over2}|CD|$.
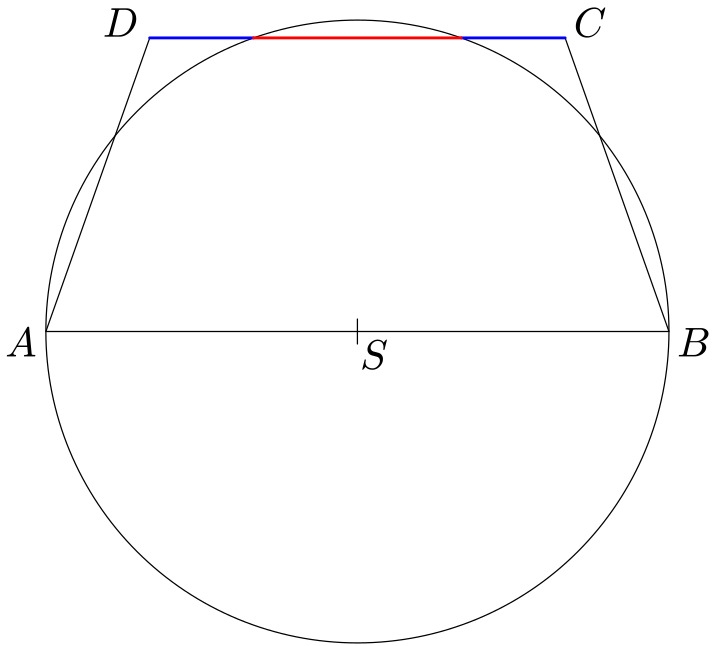
Řešení
Označme $r={1\over 2}|AB|$ poloměr kružnice, $h$ výšku lichoběžníku, $c=|EF|={1\over 2}|EG|={1\over 4}|CD|$ polovinu délky části základny $CD$ ležíci uvnitř kružnice a $a=|HD|$ délku úseku ramene $AD$ vně kružnice.

2. Řešení geometrickou úvahou. Protože $|SJ|=2c$, platí $|AJ|=c$ a trojúhelníky $EFS$ a $AJD$ jsou shodné. Tedy $|AD|=|ES|=r$. Protože obvodové úhly $EGH$ a $EAH$ nad tětivou $HE$ mají stejnou velikost a $|DA|=|DG|=r$, jsou trojúhelníky $DGH$ a $DAE$ (po převrácení) shodné. Platí tedy $a=c$, a tedy také $|AH|=|EG|=2c$. Z toho dostáváme $|AH|:|HD|=2:1$.