Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Arbelos

V úloze o Archimedových kruhových dvojčatech jsme již uvedli, že vybarvenému obrazci na obrázku se říká arbelos.

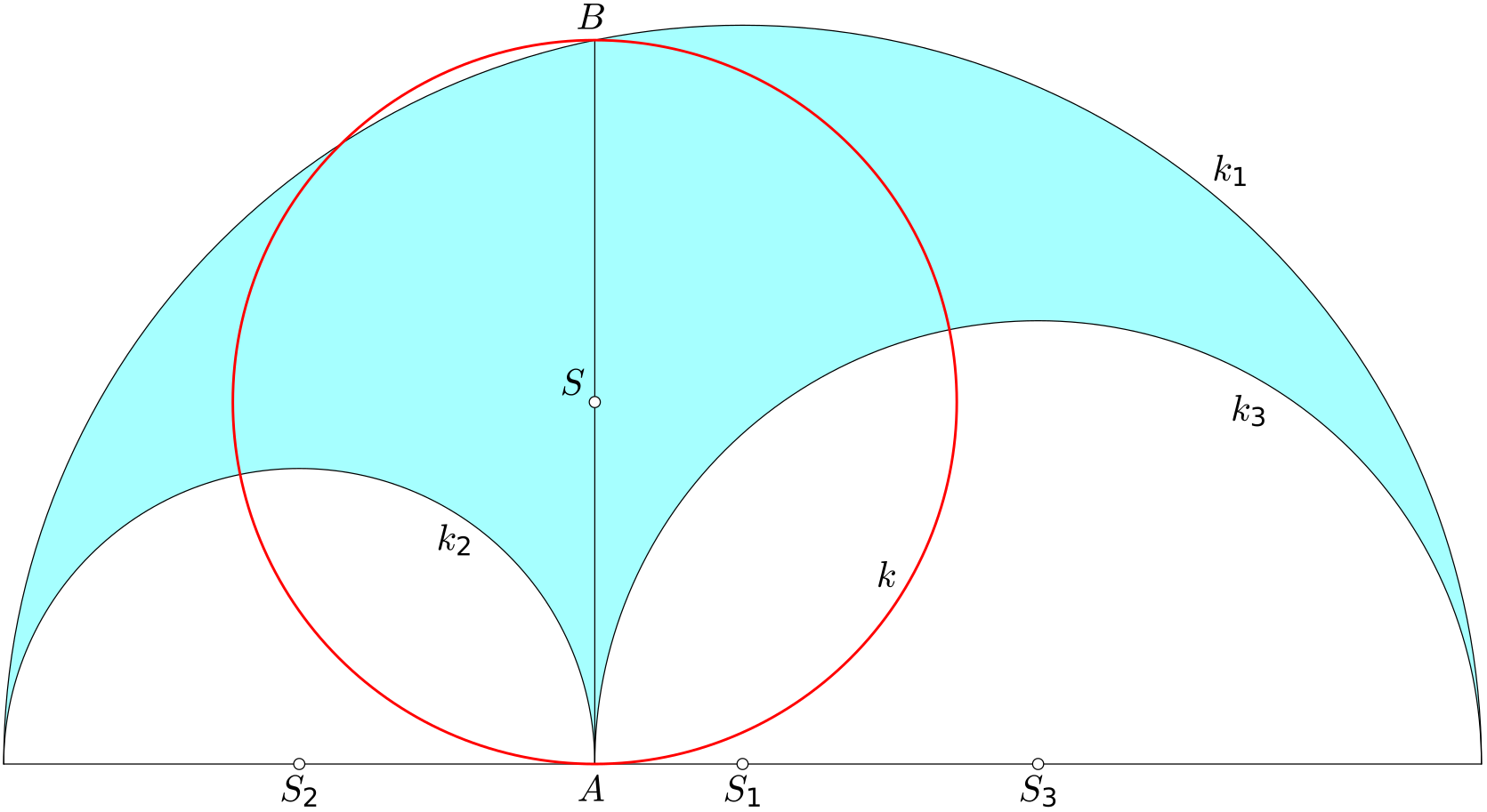
Název pochází z řečtiny, kde arbylos označuje ševcovský nůž (viz https://en.wikipedia.org/wiki/Arbelos#/media/File:Arbelos_Shoemakers_Knife.jpg).
Arbelos má jako geometrický útvar řadu pozoruhodných vlastnéstí a souvislostí. Umíte ukázat, že plošný obsah arbelu je roven obsahu kruhu ohraničeného červenou kružnicí na obrázku?

Řešení

Označme poloměry kružnic

$k_1$ ,

$k_2$ ,

$k_3$ ,

$k$ po řadě

$r_1={|CD|\over2}$ ,

$r_2={|CA|\over2}$ ,

$r_3={|AD|\over2}$ ,

$r={|AB|\over2}$ . Podle Eukleidovy věty o výšce pravoúhlého trojúhelníku platí

$|AB|^2=|CA|\cdot|AD|$ , tj.

$r^2=r_2^2\cdot r_3^2$ . (Pokud si tuto větu nepamatujete ze školy, můžete si ten vtah snadno odvodit z podobnosti pravoúhlých trojúhelníků

$CAB$ a

$BAD$ .) Obsah arbelu

$P$ je roven rozdílu obsahu půlkruhu o poloměru

$r_1$ a obsahů půlkruhů o poloměrech

$r_2$ a

$r_3$ , tj.

$P={\pi\over2}r_1^2-{\pi\over2}r_2^2-{\pi\over2}r_3^2={\pi\over2}[(r_2+r_3)^2-r_2^2-r_3^2]=\pi r_2r_3=\pi r^2$ .

Tvrzení je názorně vidět, když si uvědomíme, že obsah kruhu je přímo úměrný druhé mocnině poloměru a že tedy Pythagorovu větu lze zobecnit i tak, že místo čtverců nad přeponou a odvěsnami budeme uvažovat půlkruhy. Překlopíme půlkruh podle průměru a do dolního půlkruhu překlopíme i červený kruh.

Bílý trojúhelník na následujících obrázcích je pravoúhlý (Thaletova věta).

Pro obsahy půlkruhů tedy podle zobecněné Pythagorovy věty platí

$P_2=P_3+P_4$ ,

$P_3=P_5+P_6$ a

$P_9=P_7+P_8$ , takže

$P=P_2-P_5-P_7=P_3+P_4+P_6-P_3+P_6-P_4=2P_6=P_1$ .