Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Popularizační přednášky Zábavné úlohy Trojrozměrný kalendář na rok 2020 Česká digitální matematická knihovna Další odkazy

Úlohy pro zábavu i pro poučení

Překládáme čtverec

Vezmeme papír tvaru čtverce o straně 20 cm a přeložíme ho tak, že jeden z vrcholů umístíme do středu protější strany. Jeden roh pak bude přečnívat. Jak velký bude plošný obsah přečnívajícího trojúhelníku, který je na obrázku vybarven červeně?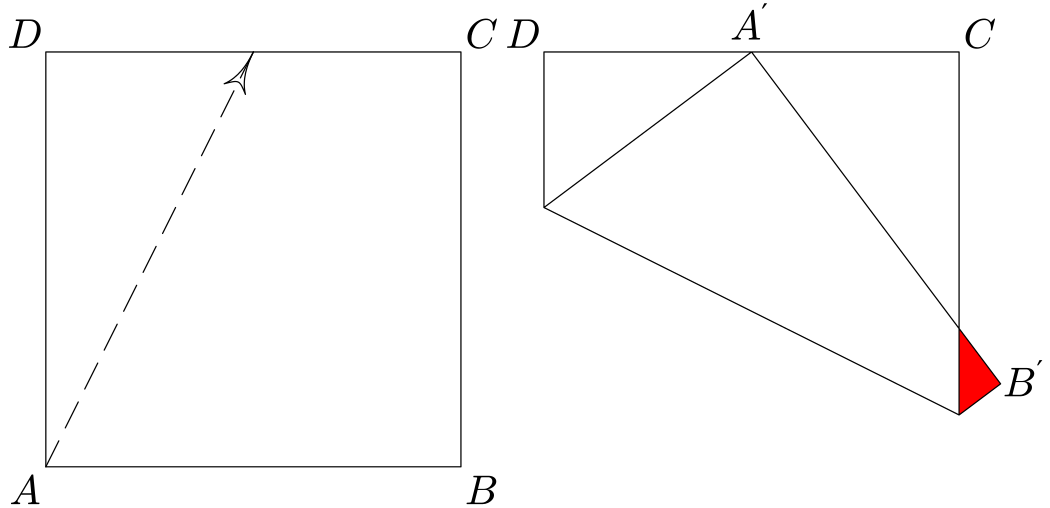

Řešení

Při označení na obrázku (pro zjednodušení zápisu vynecháme jednotky délky) v pravoúhlém trojúhelníku $EA'D$ platí $x+y=20$ a podle Pythagorovy věty také $x^2+10^2=y^2$. Odtud snadno vypočítáme, že $x={15\over2}$ a $y={25\over2}$. Úhly $EA'D$ a $A'FC$ jsou shodné, takže trojúhelníky $EA'D$, $A'FC$ jsou podobné. Platí tedy $u:10:v=10:x:y=10:{15\over2}:{25\over2}$ a z toho dostáváme $u={40\over3}$ a $v={50\over3}$. Ze stejného důvodu jsou podobné trojúhelníky $EA'D$ a $GFB'$, takže platí $t:s=x:10={15\over2}:10$, a protože $s=20-v={10\over3}$, dostáváme $t={5\over2}$. Červeně vynačený trojúhelník má tedy obsah ${1\over2}st={25\over6}$.
Úloha byla zařazena do druhého kola 40. ročníku Matematické olympiády v kategorii pro žáky 8. ročníků základních škol.