Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Z nepřeberného množství matematických úloh, které pobaví, poučí a někdy i překvapí nečekaným pohledem na realitu, každý týden vybíráme tři – často jednoduché, někdy zapeklité.Elektrikářův úkol
Elektrikář má spojit kabelem dvě místa $A$, $B$ v budově. Jsou na stejné zdi, která je však přerušena betonovým překladem (na obrázku vyznačeno šedou barvou).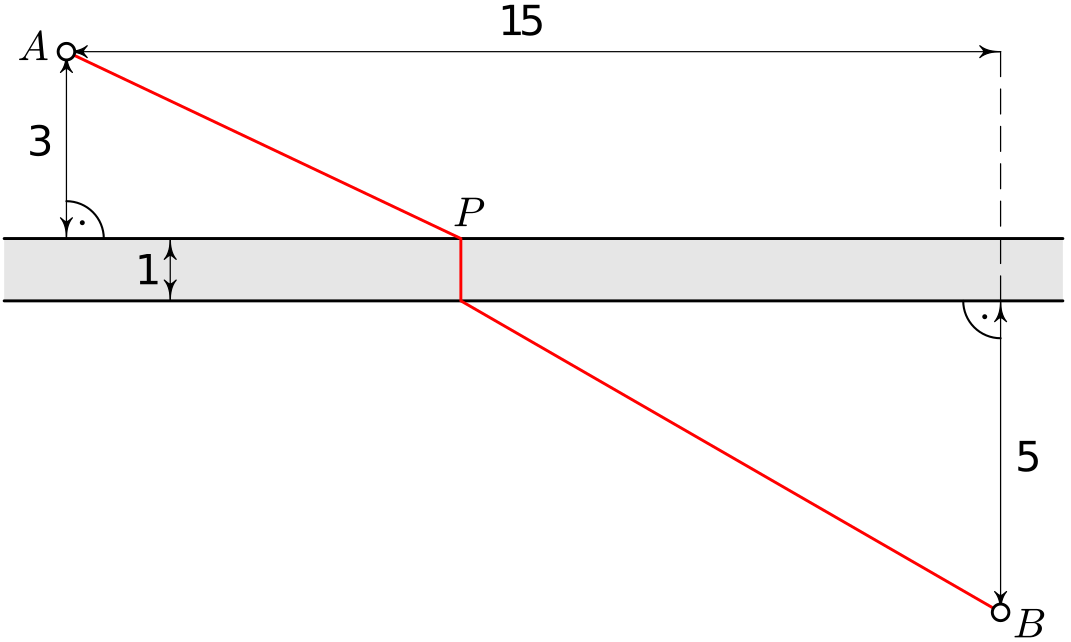
Řešení
Vyřazovací turnaj
Šachového turnaje hraného vyžazovacím systémem se účastní osm hráčů. Jeden z nich je tak silný, že bezpečně porazí kohokoli z ostatních. Další je tak silný, že bezpečně porazí kohokoli z ostatních kromě toho nejsilnějšího. Hráči jsou do prvního kola nasazeni losováním. Je jasné, že ten nejsilnější hráč v turnaji zvítězí. Druhý nejsilnější hráč však může vypadnouut už v prvním kole, pokud v něm narazí na toho nejsilnějšího. S jakou pravděposobností se druhý nejsilnější hráč dostane do finále?Řešení
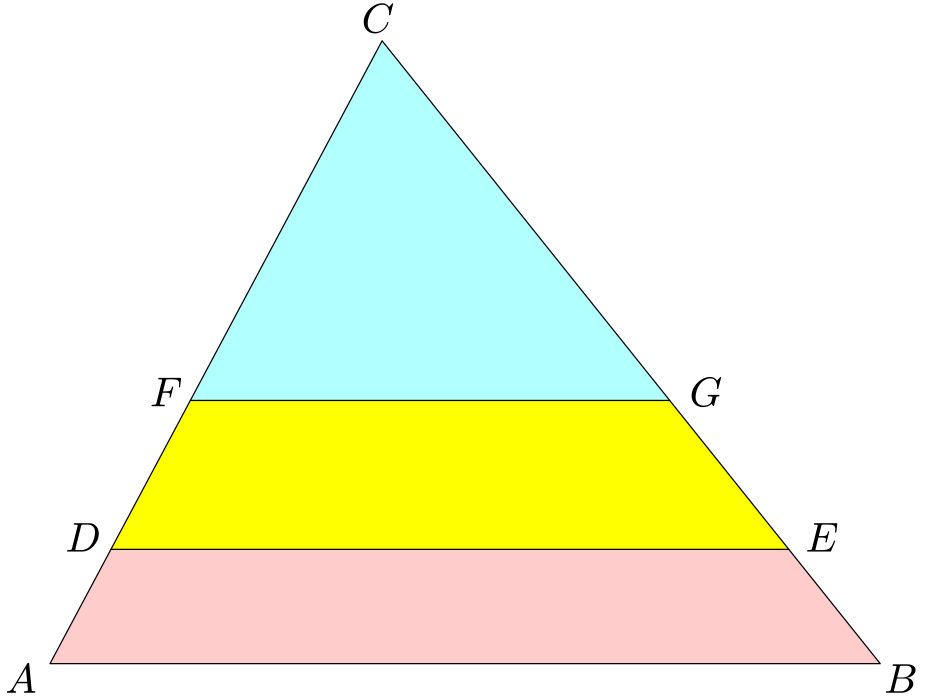
Dělení trojúhelníkové parcely
Otec chce rozdělit svou parcelu tvaru obecného trojúhelníku $ABC$ na tři díly stejného obsahu tak, aby dělící čáry byly rovnoběžné se stranou $AB$.