Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Vrcholy pravoúhlých trojúhelníků
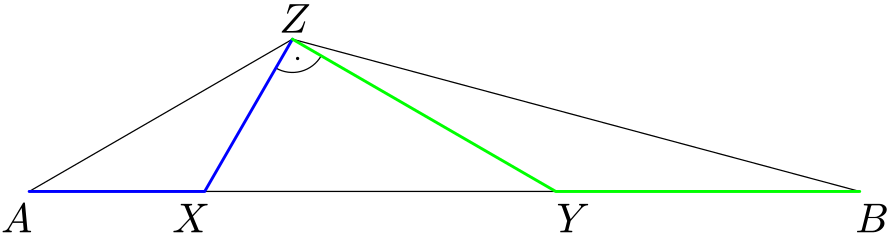
V rovině je dána úsečka $AB$. Najděte množinu všech vrcholů pravoúhlých trojúhelníků $XYZ$ těchto vlastností:
- (1) Přepona $XY$ je částí úsečky $AB$.
- (2) Pro délky odvěsen platí $|XZ|=|AX|$, $|BZ|=|BY|$.
Řešení
Uvažujme některý pravoúhlý trojúhelník požadovaných vlastností.
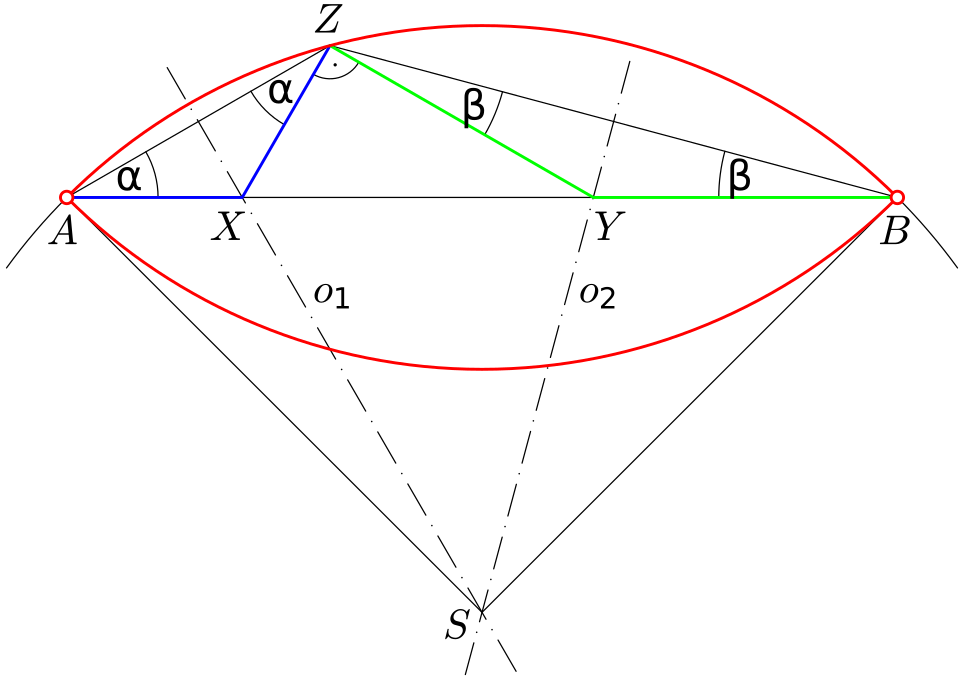
Trojúhelníky $ZAX$, $BZY$ jsou podle vlastnosti (2) rovnoramenné, takže úhly při vrcholech $A$ a $Z$, resp. $B$ a $Z$ jsou shodné. Pro součet velikostí úhlů v trojúhelníku $ABZ$ platí $\alpha+\beta+\beta+90^\circ+\alpha=180^\circ$, takže $\alpha+\beta=45^\circ$, a úhel $BZA$ má velikost $\alpha+\beta+90^\circ=135^\circ$. Vrchol $Z$ je tedy bodem, ze kterého je úsečka $AB$ vidět pod úhlem $135^\circ$, a leží tedy na (menším) kruhovém oblouku, který na kružnici opsané trojúhelníku $ABZ$ ohraničují body $A$, $B$, samozřejmě bez těchto dvou bodů. Střed $S$ kružnice sestrojíme snadno, když si uvědomíme, že úhel $ASB$ má velikost $90^\circ$. To plyne z
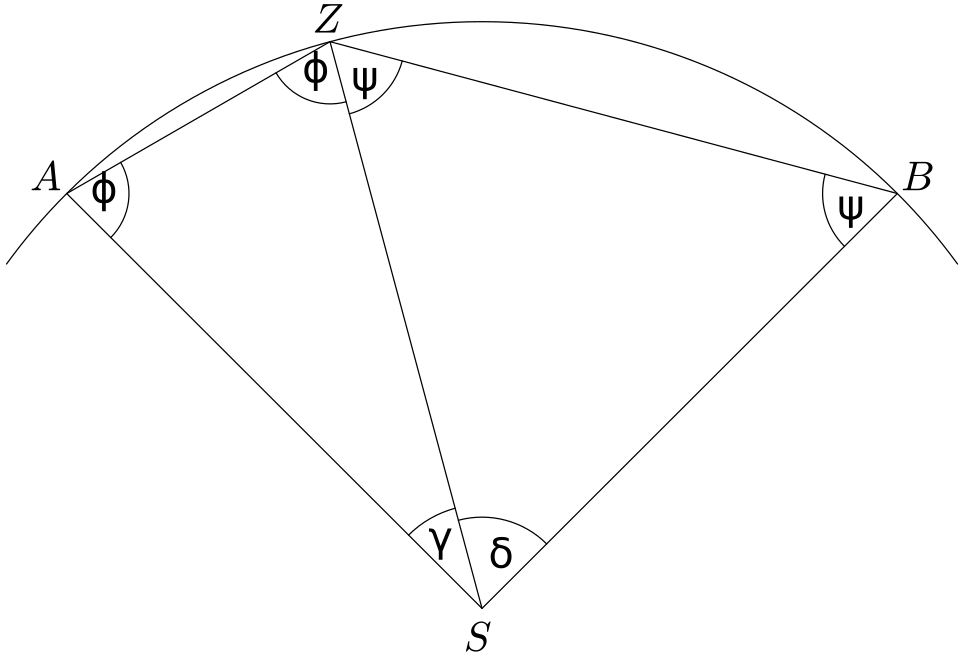
věty o obvodovém a středovém úhlu, ale můžeme to také snadno odvodit následující úvahou.
Trojúhelníky $ZAS$, $BZS$ jsou rovnoramenné. Platí tedy $\gamma=180^\circ-2\phi$, $\delta=80^\circ-2\psi$, takže $\gamma+\delta=360^\circ-2(\phi+\psi)=360^\circ-2\cdot135^\circ=90^\circ$.
Obráceně, je-li $Z$ nějaký vnitřní bod uvedeného oblouku $AB$, pak z něj je úsečka $AB$ vidět pod úhlem $135^\circ$ a osy $o_1$, $o_2$ úseček $AZ$, $BZ$ procházejí středem $S$ kružnice a protínají úsečku $AB$ v bodech $X$, $Y$, pro které platí podmínka (2). Označíme-li $\omega$ velikost úhlu $YZX$, pak $\alpha+\omega+\beta=135^\circ$ a $\alpha+\beta+\beta+\omega+\alpha=180^\circ$, takže $\omega=90^\circ$ a trojúhelník $XYZ$ je pravoúhlý.
Úloha byla zařazena do prvního kola 39. ročníku Matematické olympiády v kategorii B pro studenty středních škol.