Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Kužel a koule ve válci

Do rotačního válce o poloměru $R$ je vložen kužel, který má s válcem společnou podstavu a jehož vrchol splývá se středem horní podstavy válce. Uvnitř válce je umístěno šest stejných koulí takovým způsobem, že se každá dotýká sousedních dvou koulí, pláště kužele, pláště a horní podstavy válce. Vypočtěte poloměr $\rho$ největší koule vložené do kužele.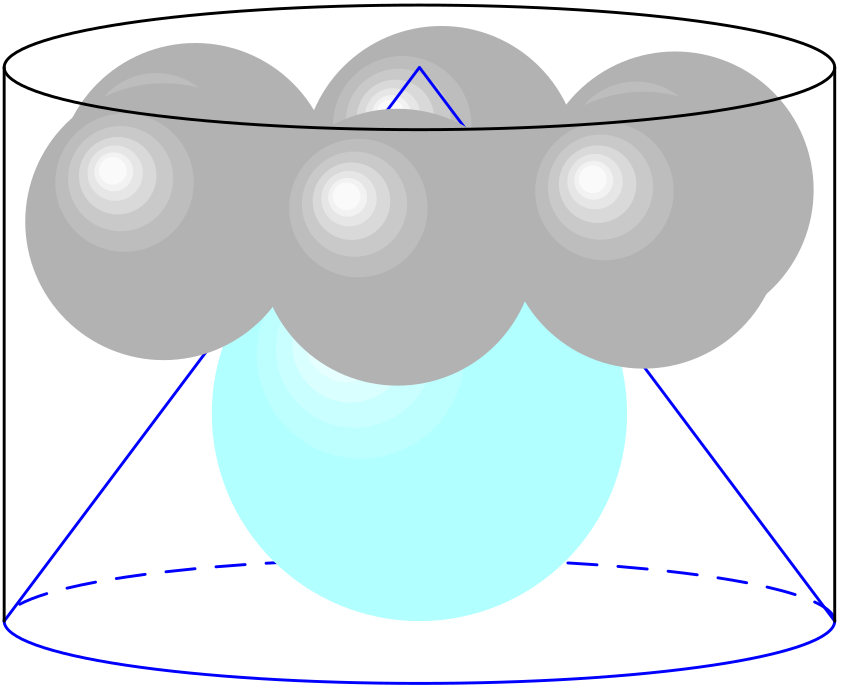

Řešení

Označme $h$ výšku válce a $r$ poloměr koulí umístěných mezi kužel a plášť válce. Podívejme se nejprve na těch šest koulí shora:

Ze symetrického uspořádání šesti koulí vyplývá velikost úhlu $\alpha=30^\circ$. Protože $|VA|=R-r$, v pravoúhlém trojúhelníku $VAB$ platí $r=|AB|=|VA|\sin 30^\circ={1\over2}(R-r)$. Odtud dostáváme $r={R\over3}$. (Jiným způsobem k tomuto výsledku dospějeme, když si uvědomíme, že trojúhelník $ABC$ je rovnostranný.)
Nyní se podívejme na svislý řez válcem vedený jeho osou a osou jedné ze šesti koulí.

Protože $|AM|=|AL|=h-r$ a $|CK|=|CM|=R-r$, podle Pythagorovy věty pro pravoúhlý trojúhelník $ABC|$ platí $R^2+h^2=(R-r+h-r)^2=({R\over3}+h)^2$. Odtud dostáváme $h={4\over3}R$. Podle Pythagorovy věty pro pravoúhlý trojúhelník $CDS$ platí $\rho^2+(h-r-R+R-r)^2=(h-\rho)^2$. Dosadíme za $h$ a $r$ a vypočteme $\rho={r\over2}$.
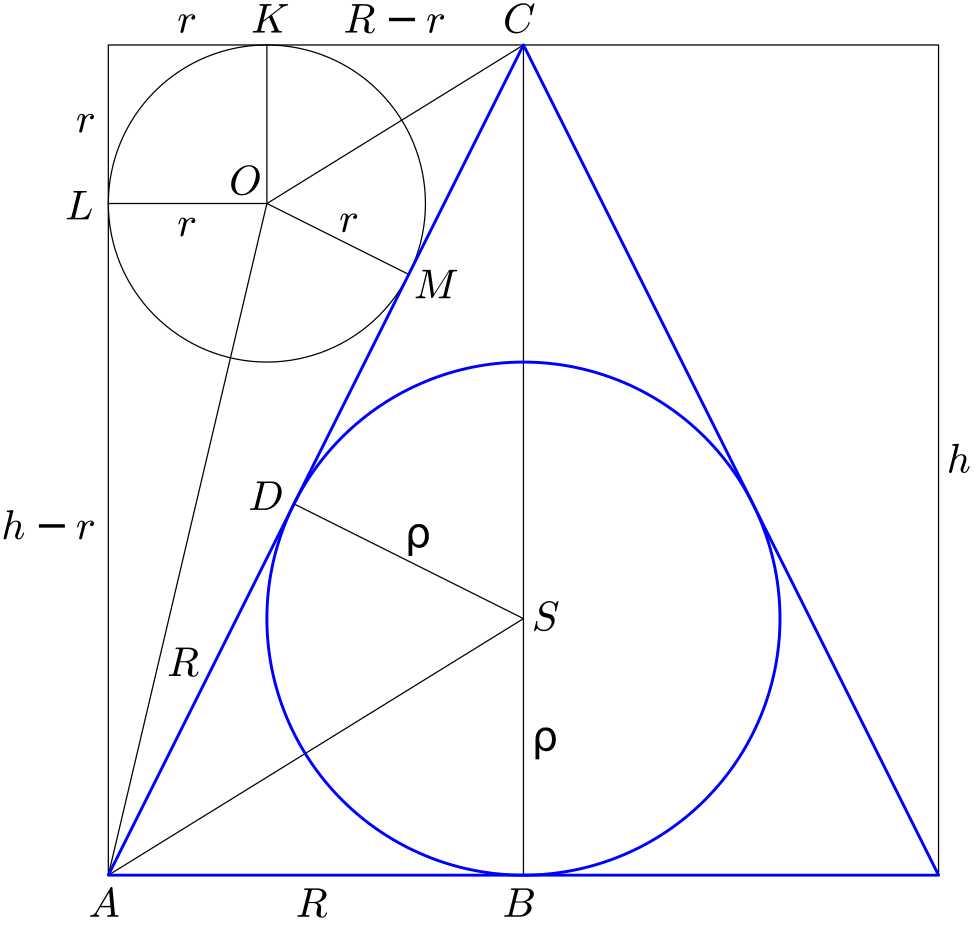
Vypočtené hodnoty ukazují, že náčrt řezu válce výše nebyl přesný. Ve skutečnosti se šest koulí dotýká koule vložené do kužele: