Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Japonský chrám

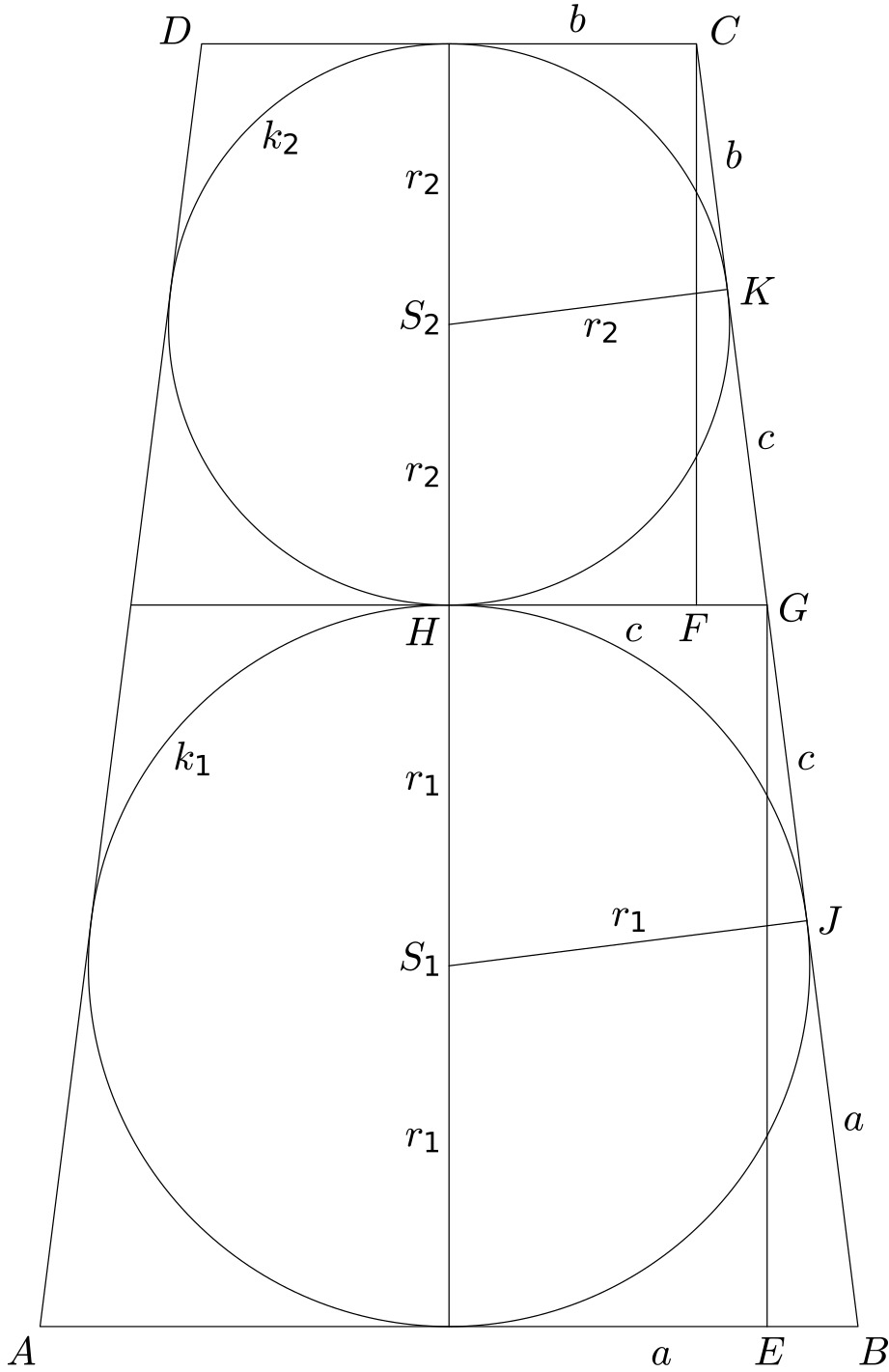
Tohle je další z historické sbírky japonských úloh san gaku. Lichoběžník

$ABCD$ je opsán dvěma dotýkajícím se kružnicím

$k_1$ ,

$k_2$ . Jeho základny mají délky

$|AB|=2a$ ,

$|CD|=2b$ .

Určete velikosti poloměrů

$r_1$ ,

$r_2$ obou kružnic.

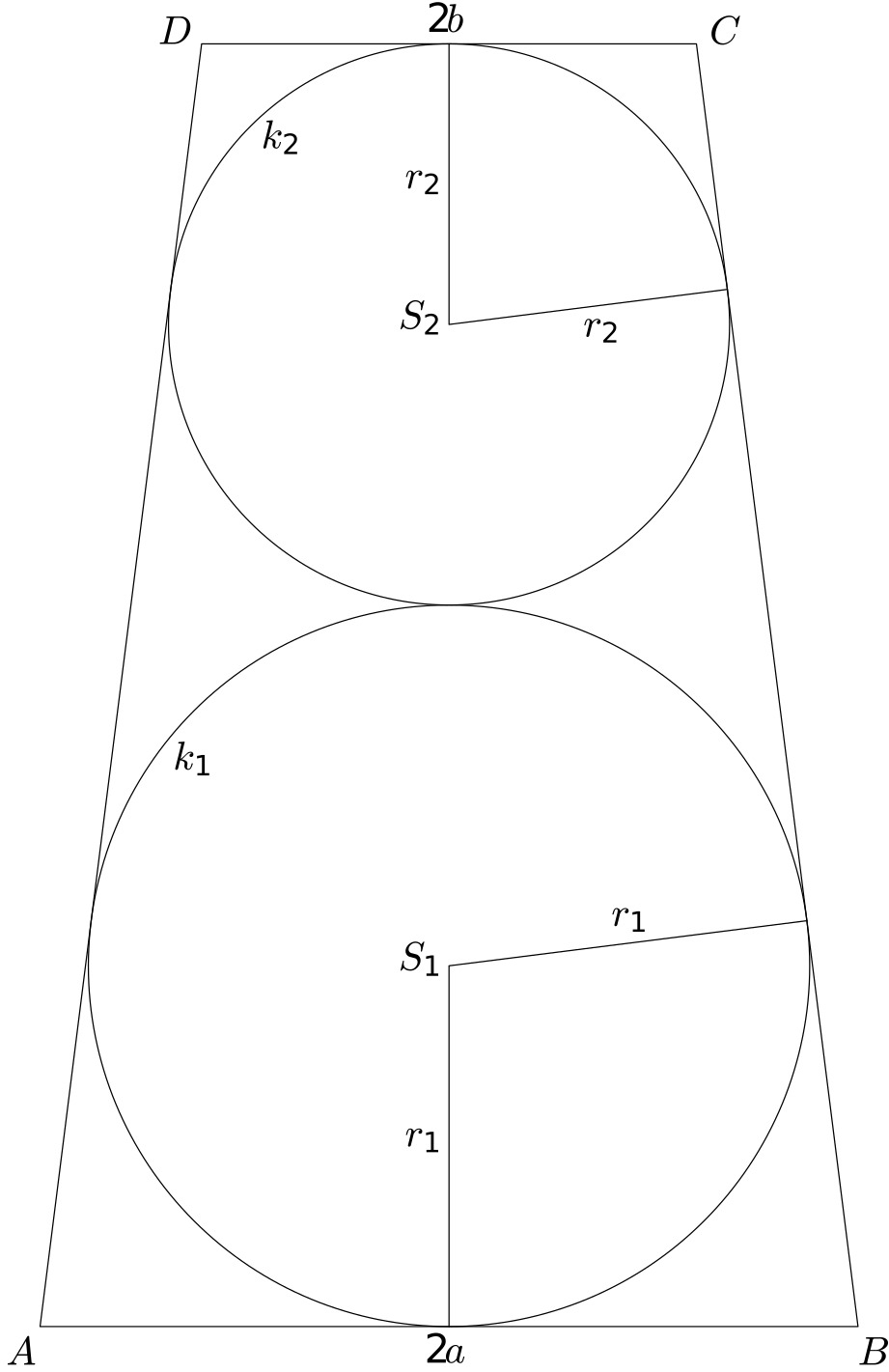
Řešení

Označme

$c=|HG|$ .

Protože

$|BJ|=a$ ,

$|JG|=c$ a

$|EB|=a-c$ , podle Pythagorovy věty pro trojúhelník

$EBG$ platí

$(a-c)^2+(2r_1)^2=(a+c)^2$ . Odtud po úpravě dostaneme

$r_1=\sqrt{ac}$ .

Obdobně pro trojúhelník

$FGC$ platí

$(c-b)^2+(2r_2)^2=(b+c)^2$ , a tedy

$r_2=\sqrt{bc}$ . Z toho plyne

${r_1\over r_2}=\sqrt{a\over b}$ . Trojúhelníky

$EBG$ a

$FGC$ jsou podobné, takže platí

${2r_1\over a+c}={2r_2\over b+c}$ tj.

${r_1\over r_2}={b+c\over a+c}$ . Dostáváme

${a\over b}={(b+c)^2\over (a+c)^2}$ a odtud po úpravě

$c=\sqrt{ab}$ , takže

$r_1=\root 4 \of {a^3b}$ a

$r_2=\root 4 \of {b^3a}$ .