Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

San gaku 1

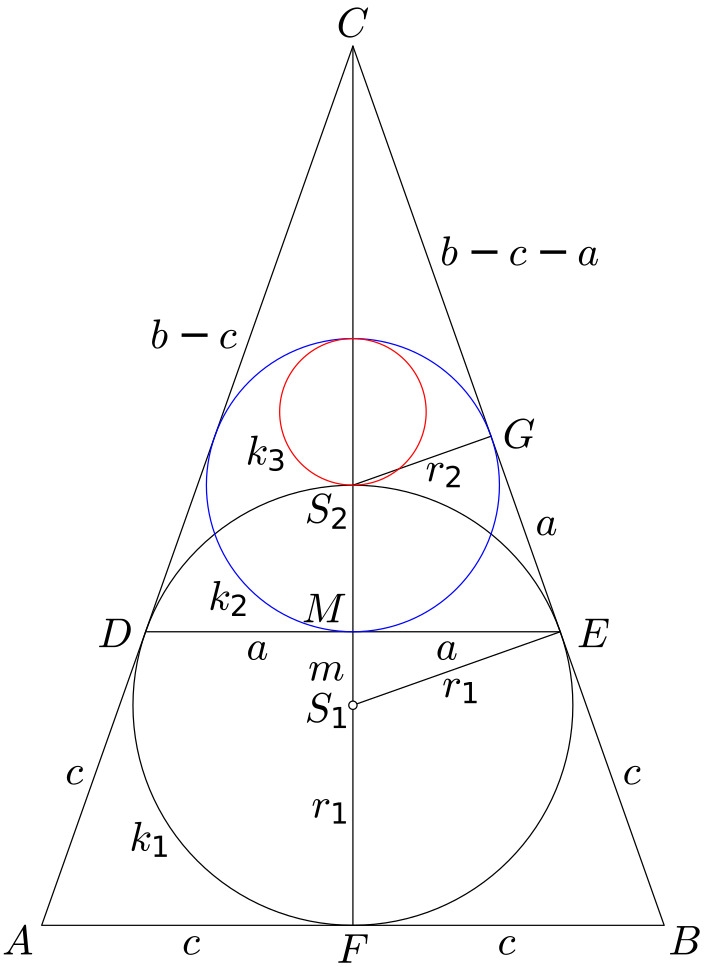
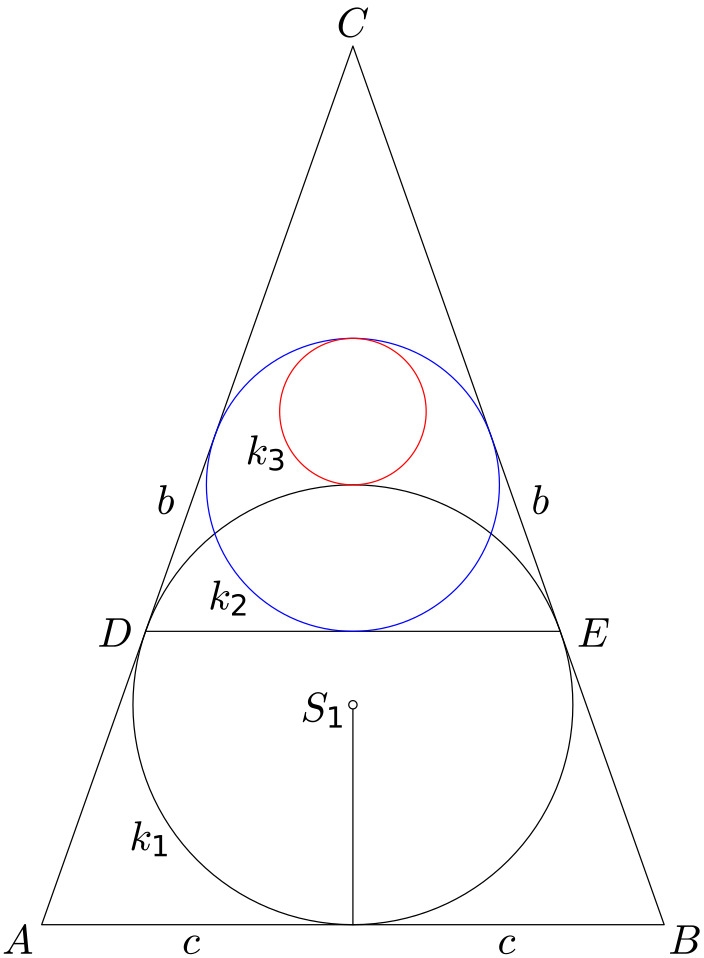
San gaku jsou japonské geometrické úlohy a tvrzení, které byly během éry Edo v 17. až 19. století malovány na dřevěné desky a věnovány šintostickým svatyním a budhistickým chrámům jako oběť nebo jako úlohy pro mnichy. Toto je příklad:

Mějme rovnoramenný trojúhelník $ABC$ s délkami stran $b=|AC|=|BC|$ a $2c=|AB|$. Trojúhelník má vepsanou kružnici $k_1$ o poloměru $r_1$, která se dotýká stran $AC$, $BC$ trojúhelníku v bodech $D$, $E$. Trojúhelníku $DEC$ je obdobně vepsána kružnice $k_2$ o poloměru $r_2$. Kružnice $k_3$ o poloměru $r_3$ se dotýká obou kružnic $k_1$, $k_2$ (viz obrázek).

Určete poměr poloměrů $r_2 : r_3$.

Řešení

Označme $S_1$ a $S_2$ středy kružnic $k_1$ a $k_2$. Z obrázku se zdá, že bod dotyku kružnic $k_1$, $k_3$ splývá se sředem kruzníce $k_2$. Nemůžeme však věřit jen obrázku, musíme to dokázat. Pro úseky tečen platí $|AD|=|AF|=c$, $|DL|=|DG|=a$ a $|CD|=|CE|=b-c$. Z podobnosti trojúhelníků $AFC$, $DMC$ plyne ${b-c\over a}={b\over a}$, a tedy $a={(b-c)c\over b}$. Obdobně platí ${b-c-a\over r_2}={b-c\over r_1}$, a tedy $r_2={(b-c-a)r_1\over b-c}={(b-c-{(b-c)c\over b})r_1\over b-c}=r_1-{r_1c\over b}$. Z podobnosti trojúhelníků $FBC$ a $MS_1E$ plyne ${m\over r_1}={c\over b}$, tj. ${r_1c\over b}=m$. Dostáváme $m+r_2={r_1c\over b}+r_1-{r_1c\over b}=r_1$, tj. vzdálenost bodů $S_2$, $S_1$ je $r_1$. Bod $S_2$ je tedy bodem dotyku kružnic $k_1$ a $k_2$, a protože je také středem kružnice $k_2$, platí $r_2=2r_3$.