Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Pythagorova věta

Pythagorova věta je matematické tvrzení, které zná (nebo o něm alespoň slyšel) snad každý, kdo prošel základním vzděláním: obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Existuje celá řada důkazů, viz např. tento obrázek:

Jiný důkaz pochází od neméně slavného řeckého matematika Eukleida.

Výše uvedená formulace Pythagorovy věty však neříká nic o tom, že tato věta platí pouze pro pravoúhlé trojúhelníky. Umíte to dokázat?

Řešení

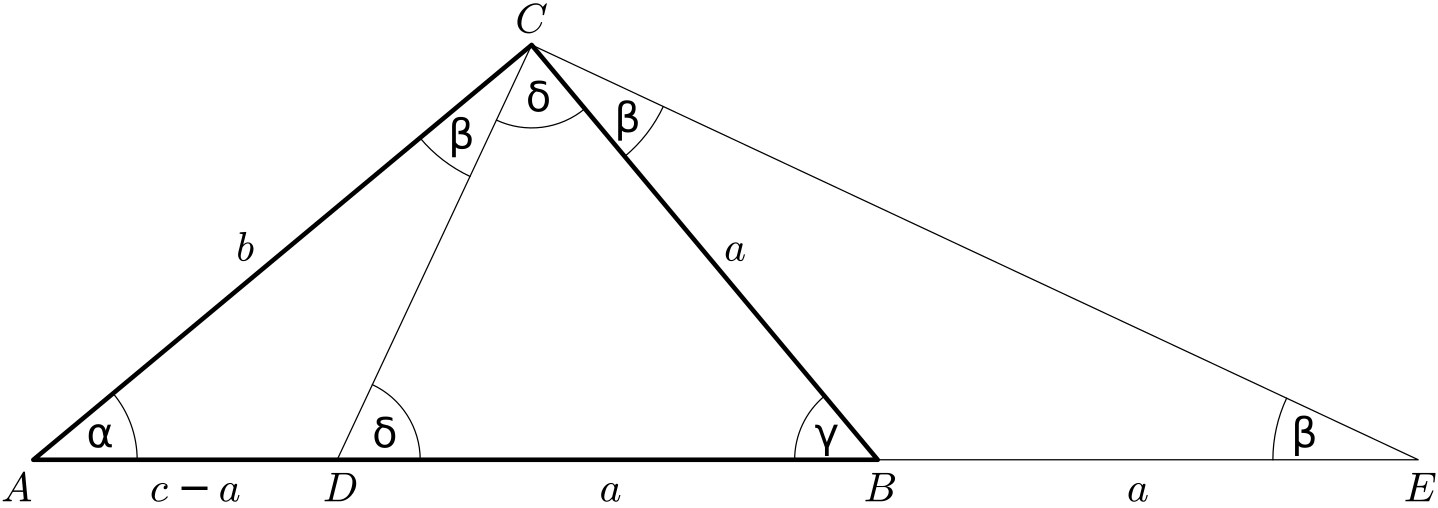
Uvažujme libovolný trojúhelník $ABC$, pro délky jehož stran $a=|BC|$, $b=|AC|$, $c=|AB|$ platí $a^2+b^2=c^2$, tj. $b^2=c^2-a^2=(c+a)(c-a)$. Na přímce $AB$ sestrojíme body $D$, $E$ ve vzdálenosti $a$ od bodu $B$ tak, že bod $D$ leží mezi body $A$, $B$ a bod $E$ leží na opačné straně od bodu $B$ než bod $A$. Pak $|AE|=c+a$ a $|AD|=c-a$.

Trojúhelníky $ADC$ a $ACE$ mají společný úhel $\alpha$ a pro délky jejich stran ze vztahu $b^2=(c+a)(c-a)$ dostaneme ${b\over c+a}={c-a\over b}$. Podle věty sus jsou tedy trojúhelníky $ADC$ a $ACE$ podobné, a tedy jejich úhly při vrcholech $C$ a $E$ mají stejnou velikost $\beta$. Trojúhelník $ECB$ je rovnoramenný, takže jeho úhel při vrcholu $C$ má také velikost $\beta$. Z toho plyne $\gamma=2\beta$, a protože trojúhelník $DBC$ je také rovnoramenný, platí $\delta={1\over2}(180^\circ-\gamma)=90^\circ-\beta$, a tedy úhel v trojúhelníku $ABC$ při vrcholu $C$ má velikost $\beta+\delta=90^\circ$.