Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Menelaova věta

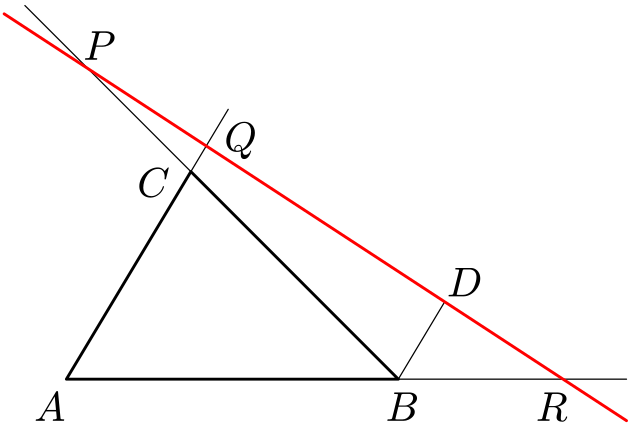
Menelaos z Alexandrie (asi 70–140 n. l.) byl řecký matematik a astronom. Byl prvním, kdo definoval sférický trojúhelník (geometrický útvar na povrchu koule určený třemi hlavními kružnicemi; na kulovém glóbu ho např. tvoří dva poledníky a rovník). Připisuje se mu následující věta. V rovině je dán trojúhelník

$ABC$ a tři body

$P$ ,

$Q$ ,

$R$ ležící na přímkách

$BC$ ,

$AC$ a

$AB$ . Jestliže tyto body leží na téže přímce, pak platí

${AR\over RB}\cdot{BP\over PC}\cdot{CQ\over QA}=-1$ , kde

$XY\over YZ$ označuje podíl délek úseček

$XY$ a

$YZ$ se znaménkem plus, je-li bod

$Y$ mezi body

$X$ ,

$Z$ , a v opačném případě se znaménkem minus. Mohou nastat dva případy podle toho, jestli přímka

$PR$ protíná trojúhelník

$ABC$

nebo ne

Menelaos uměl větu dokázat před dvěma tisíci lety. Umíte to také?

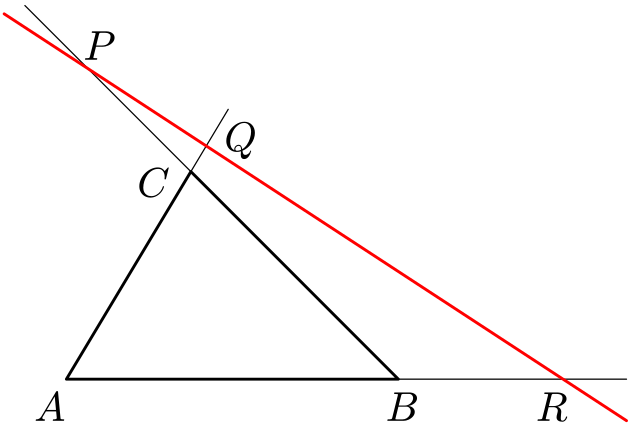
Řešení

Označme

$D$ průsečík rovnoběžky s přímkou

$AC$ vedenou bodem

$B$ a přímky

$PR$ .

Z podobnosti trojúhelníků

$BRD$ a

$ARQ$ plyne

${|BD|\over|QA|}={|RB|\over|AR|}$ a z podobnosti trojúhelníků

$DPB$ a

$QPC$ plyne

${|BD|\over|CQ|}={|BP|\over|PC|}$ . Odtud dostáváme

$|BD|={|QA|\cdot|RB|\over|AR|}={|CQ|\cdot|BP|\over|PC|}$ , tj.

${|AR|\over|RB|}\cdot{|BP|\over|PC|}\cdot{|CQ|\over|QA|}=1$ . Přiřadíme-li jednotlivým podílům znaménka podle vzájemné polohy bodů dle zadání, bude výraz

${AR\over RB}$ se znaménkem mínus a výrazy

${BP\over PC}$ ,

${CQ\over QA}$ se znaménkem plus, takže dostaneme

${AR\over RB}\cdot{BP\over PC}\cdot{CQ\over QA}=-1$ . Zcela stejně postupujeme ve druhém případě: