Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Půlkruh v lichoběžníku

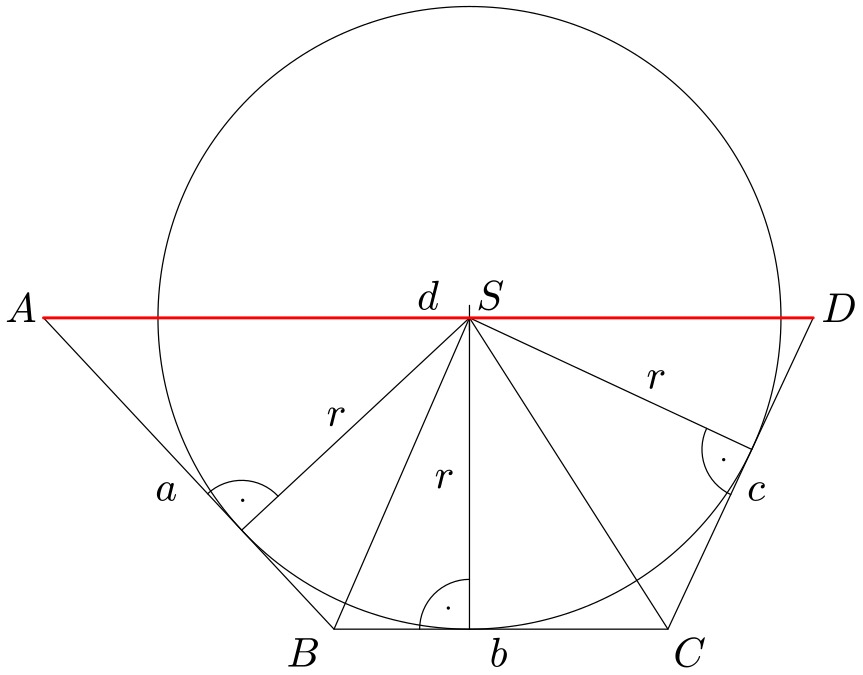
Lichoběžník

$ABCD$ má tu vlastnost, že střed kružnice dotýkající se základny

$BC$ a ramen

$AB$ ,

$CD$ leží na základně

$CD$ . Určete délku základny

$|CD|=d$ , jsou-li dány délky ramen

$|AB|=a$ ,

$|CD|=c$ .

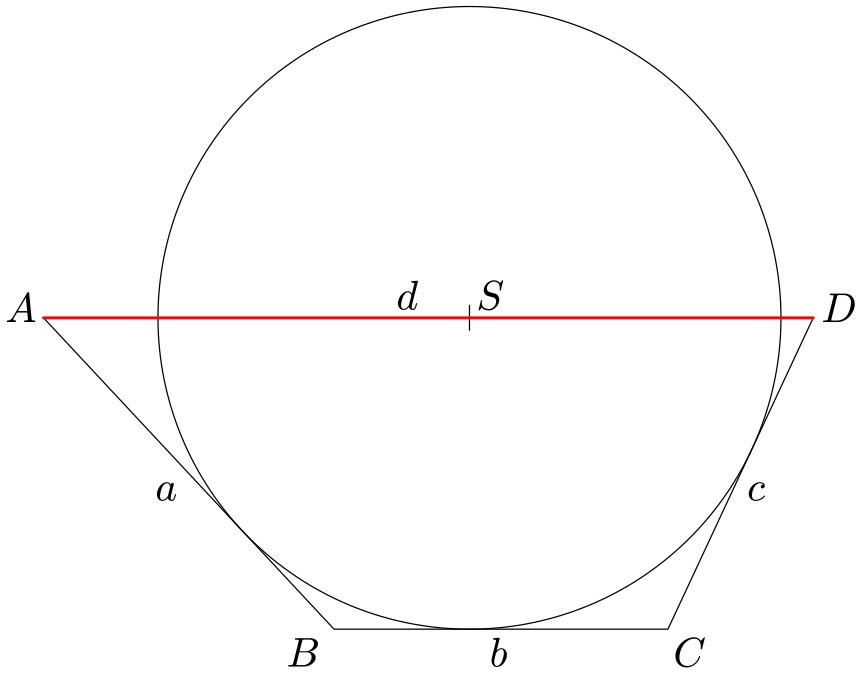
Řešení

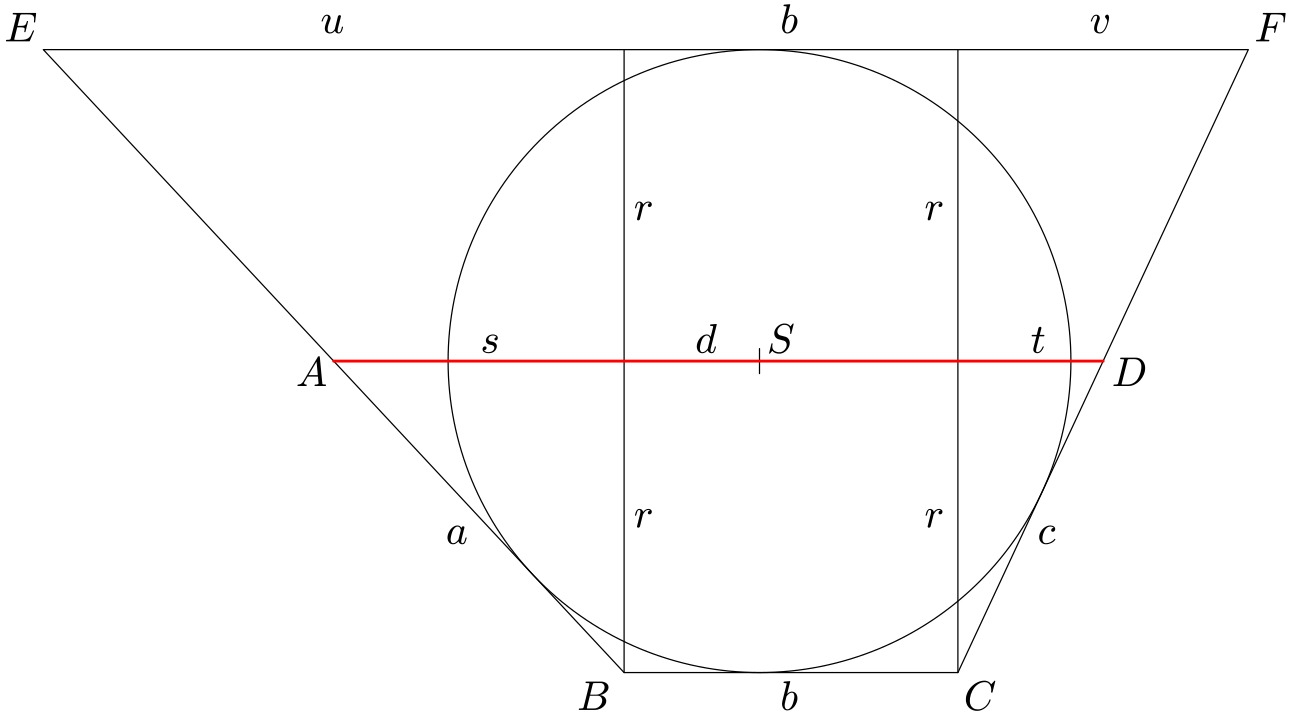
1. řešení. Ke kružnici vedeme tečnu rovnoběžnou se základnou

$BC$ a sestrojíme lichoběžník

$EBCF$ . V bodech

$B$ ,

$C$ vztyčíme výšky lichoběžníku

$ABFE$ .

Z podobnosti trojúhelníků plyne

${s\over r}={u\over 2r}$ a

${t\over r}={v\over 2r}$ , tj.

$u=2s$ a v=2t

$. Protože čtyřúhelník$ EBCF

$je tečnový, platí, že součty délek jeho protilehlých stran jsou stejné:$ 2a+2c=b+u+b+v

$. Po dosazení za$ u

$a$ v

$dostaneme$ 2a+2c=2b+2s+2t

$, tj.$ b+s+t=a+c

$. Odtud již plyne, že$ d=s+b+t=a+c$.

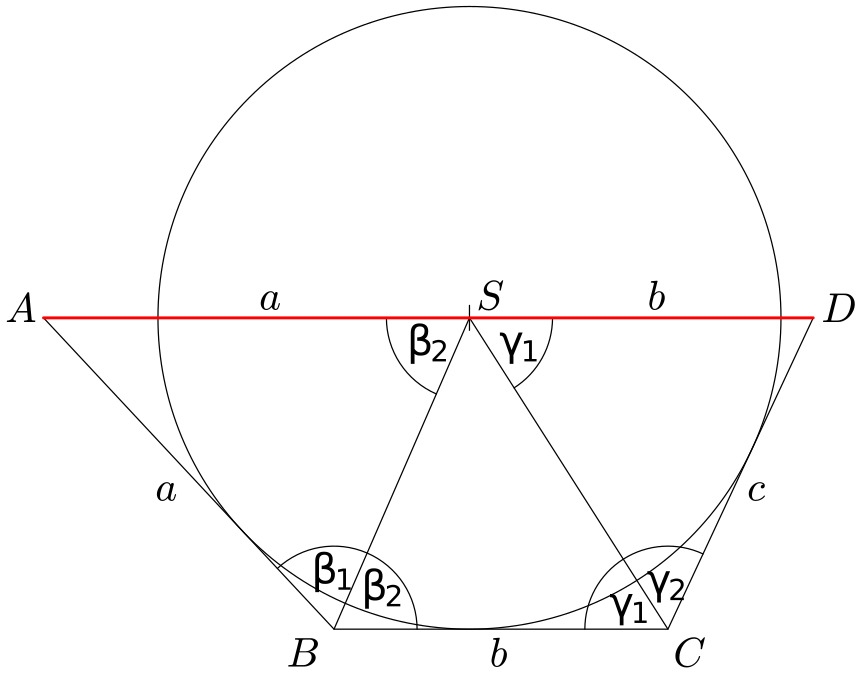
2. řešení. Protože přímky $BC$ a $AD$ jsou rovnoběžné, platí $\beta_1=\beta_2$ a $\gamma_1=\gamma_2$ , a tedy trojúhelníky $BSA$ a $SCD$ jsou rovnoramenné.

Dostáváme

$d=a+c$ .

3. řešení. Výška lichoběžníku $ABCD$ je rovna poloměru $r$ dané kružnice. Jeho obsah lze tedy vyjádřit jako $O={1\over2}(b+d)r$ . Zároveň platí, že všechny tři trojúhelníky $ABS$ , $BCS$ a $CDS$ mají výšku velikosti $r$ . Obsah lichoběžníku lze tedy vyjádřit jako součet obsahů těchto tří trojúhelníků: $O={1\over2}ar+{1\over2}br+{1\over2}cr$ .

Srovnáním obou vztahů dostáváme

${1\over2}r(b+d)={1\over2}r(a+b+c)$ a odtud již plyne

$d=a+c$ .