Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Na jih, na východ, na sever a zpět
Člověk vyrazí na jih, po jednom kilometru zahne na východ, po dalším kilometru zahne na sever a octne se ve výchozím bodu. Kde na Zemi je takový výchozí bod?
Řešení
V rovině něco takového není možné, protože by ty tři kilometrové úseky tvořily tři strany čtverce a začátek a konec cesty by se neshodovaly. Na povrchu Země, který je zakřivený, to však možné je.
Severní pól je takovým výchozím bodem. Člověk z něj vyrazí na jih po poledníku. Pak pokračuje na východ po rovnoběžce a zůstává po celou dobu ve vzdálenosti $1~\text{km}$ od severního pólu. Když pak zahne na sever, dorazí po jednom kilometru na severní pól.
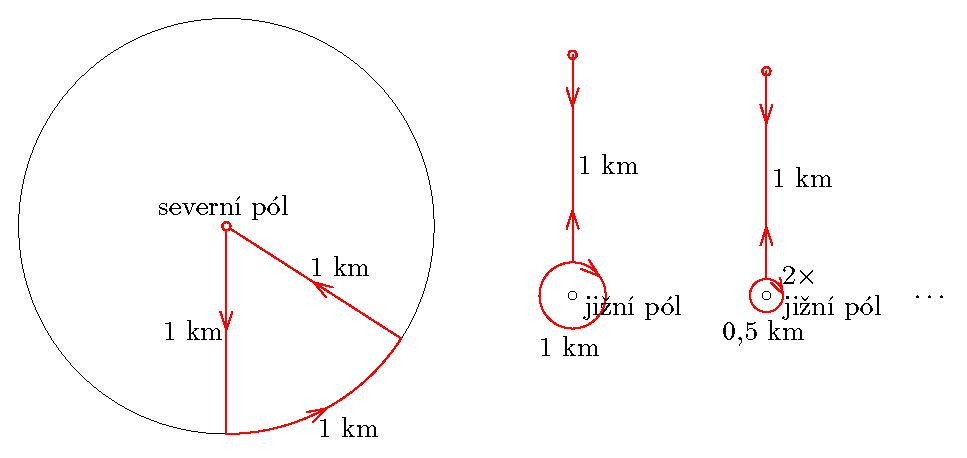
To bylo snadné. Je to však jediný bod na Zemi s takovou vlastností? Ve skutečnosti existuje nekonečné množství dalších bodů s uvedenou vlastností. Všechny leží v blízkosti jižního pólu. Uvažme např. rovnoběžku na jižní polokouli, jejíž poloměr je roven ${1\over2\pi}~\text{km} \approx 0,159155~\text{km}$ a kterýkoli bod ve vzdálenosti $1~\text{km}$ na sever od ní. Po jednom kilometru cesty na jih z tohoto bodu člověk dorazí na uvedenou rovnoběžku. Délka kružnice tvořící tuto rovnoběžku je $2\pi\cdot{1\over2\pi}~\text{km}=1~\text{km}$, takže po $1~\text{km}$ chůze východním směrem ji člověk celou projde a dorazí do stejného bodu, ve kterém rovnoběžku začal procházet. Zahne na sever a stejnou cestou se vrátí do výchozího bodu.
Hledaných bodů je však ještě mnohem více. Místo uvedené rovnoběžky můžeme vzít kteroukoli rovnoběžku na jižní polokouli o poloměru ${1\over2n\pi}~\text{km}$, kde $n$ je libovolné přirozené číslo. Délka takové rovnoběžky je $2\pi\cdot {1\over2n\pi}~\text{km}= {1\over n}~\text{km}$, takže když ji člověk projde celkem $n$-krát, urazí přesně $1~\text{km}$ východním směrem a dojde do bodu, ve kterém ji začal procházet. Nyní zahne na sever a po $1~\text{km}$ se vrátí do výchozího bodu.
