Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Co je větší?
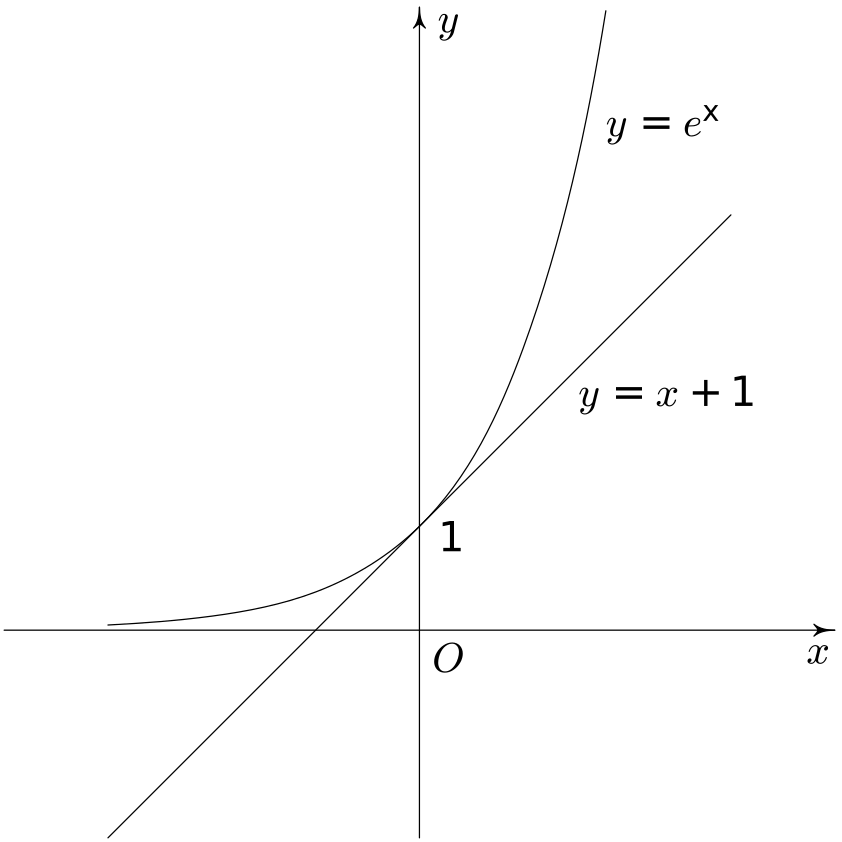
Rozhodnout, které z čísel $a^b$ a $b^a$ je větší, je v některých případech snadné, např. pro $a=2$ a $b=3$. V případě, že se čísla $a$, $b$ příliš neliší, to tak snadné být nemusí. Jak je tomu v případě $a=\pi$, $b=e$, kde $e$ je Eulerova konstanta (základ přirozeného logaritmu).Řešení
Když zkusíme dosadit přibližné hodnoty $3{,}14$ za $\pi$ a $2{,}72$ za $e$, budou se obě mocniny lišit tak málo, že podle toho nemůžeme s jistotou rozhodnout, které z čísel $\pi^e$, $e^\pi$ je větší. K rozhodnutí budeme potřebovat trochu pokročilejších středoškolských znalostí. Pro každé reálné číslo $x$ platí $e^x>1+x$: