Matematika pro poučení i pro zábavu
Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943
Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006
Úlohy pro zábavu i pro poučení
Elektrikářův úkol
Elektrikář má spojit kabelem dvě místa $A$, $B$ v budově. Jsou na stejné zdi, která je však přerušena betonovým překladem (na obrázku vyznačeno šedou barvou).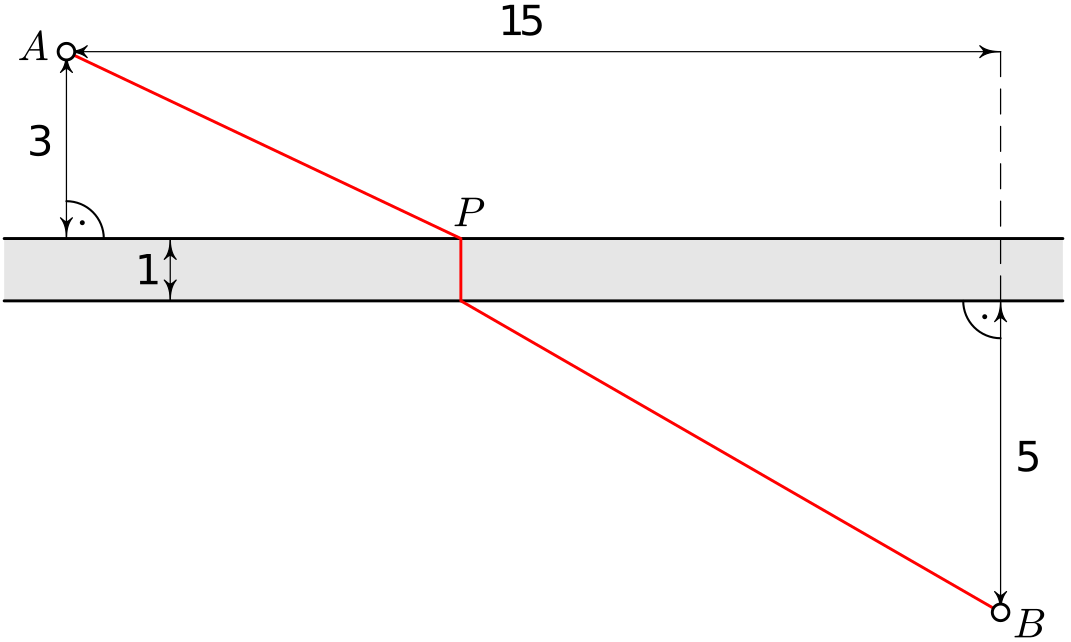
Řešení
Kdo se pokusil řešit úlohu analytickým vyjádřením délky kabelu a hledáním minima, ten se asi trochu zapotil. Elektrikář s praxí a představivostí to dokáže jednodušeji. Představme si, že by překlad nebyl mezi body $A$, $B$, ale těsně pod bodem $B$: