Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Vyřazovací turnaj

Šachového turnaje hraného vyžazovacím systémem se účastní osm hráčů. Jeden z nich je tak silný, že bezpečně porazí kohokoli z ostatních. Další je tak silný, že bezpečně porazí kohokoli z ostatních kromě toho nejsilnějšího. Hráči jsou do prvního kola nasazeni losováním. Je jasné, že ten nejsilnější hráč v turnaji zvítězí. Druhý nejsilnější hráč však může vypadnouut už v prvním kole, pokud v něm narazí na toho nejsilnějšího. S jakou pravděposobností se druhý nejsilnější hráč dostane do finále?

Řešení

Na obrázku je znázorněn turnajový pavouk.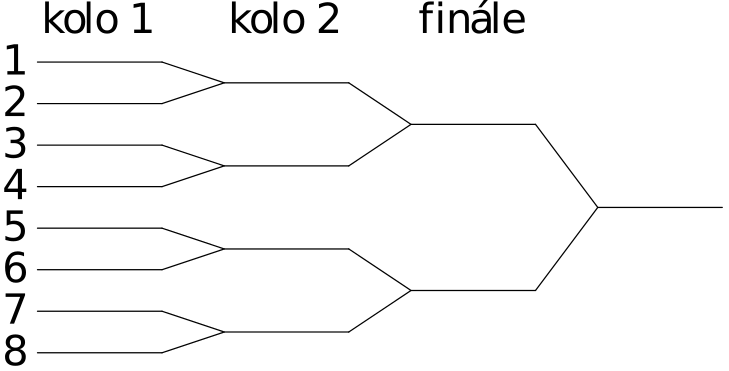

Je zřejmé, že druhý hráč se dostane do finále jen tehdy, když bude do prvního kola nasazen v jiné polovině pavouka než nejsilnější hráč (bude-li nejsilnější hráč na některém z míst 1-4, musí být druhý nejsilnější hráč na některém z míst 5-8). Druhý nejsilnější hráč může být na nasazen na něteré ze sedmi míst, která nejsou obsazena nejsilnějším hráčem. Místa, ze kterých se dostane do finále, jsou čtyři. Do finále se tedy dostane s pravděpodobností ${4\over7}>{1\over2}$.
Obecně, hraje-li turnaj $2^n$ hráčů, může být druhý nejsilnější hráč nasazen na některé z $2^n-1$, ale do finále se dostane z některého z té poloviny míst, v níž není nasazen nejsilnější hráč; takových míst je $2^{n-1}$. Pravděpodobnost toho, že se dostane do finále, je tedy při náhodném losování rovna ${2^{n-1}\over2^n-1}={1\over2-{1\over2^{n-1}}}$. To je stále víc než ${1\over2}$. Je však vidět, že s rostoucím počtem hráčů pravděppdobnost klesá a blíží se k ${1\over2}$.