Matematika pro poučení i pro zábavu

Nedělejte si starosti ohledně vašich potíží v matematice. Můžu vás ujistit, že ty moje jsou ještě větší.
Albert Einstein v dopise středoškolačce Barbaře Lee Wilsonové 7. 1. 1943

Matematika je krásná: Co bylo pravda včera, je pravda i dnes.
Jaroslav Kurzweil při převzetí České hlavy v r. 2006

Úlohy pro zábavu i pro poučení

Dělení trojúhelníkové parcely

Otec chce rozdělit svou parcelu tvaru obecného trojúhelníku

$ABC$ na tři díly stejného obsahu tak, aby dělící čáry byly rovnoběžné se stranou

$AB$ .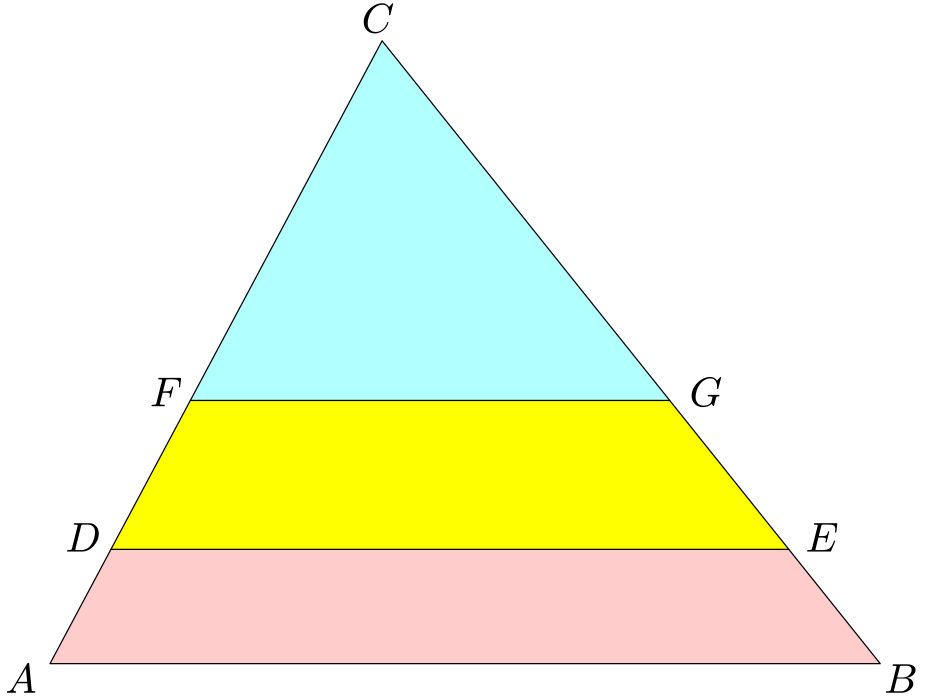

V jaké vzdálenosti od strany

$AB$ má vést dělicí čáry

$DE$ ,

$FG$ ?

Řešení

Označme

$K$ patu kolmice z vrcholu

$C$ na stranu

$AB$ a

$L$ ,

$M$ průsečíky výšky

$CK$ s příčkami v trojúhelníku rovnoběžnými se stranou

$AB$ .

Označme

$v$ délku výšky

$CK$ . Z podobnosti trojúhelníků

$ABC$ ,

$FGC$ plyne

$|FG|:|AB|=|GC|:|BC|$ a z podobnosti trojúhelníků

$KBC$ ,

$MGC$ plyne

$|CM|:v=|GC|:|BC|$ . Protože obsah trojúhelníku

$FGC$ má být třetinou obsahu trojúhelníku

$ABC$ , musí platit

$|FG|\cdot|CM|={1\over3}|AB|\cdot v$ . Odtud snadno vypočteme

$|CM|={\sqrt3\over3}v$ . Odbobným způsobem vypočteme

$|CL|={\sqrt6\over3}v$ , takže

$|KL|=(1-{\sqrt6\over3})v$ a

$|LM|={\sqrt6-\sqrt3\over3}v$ .