Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Paradoxní skládačka podruhé

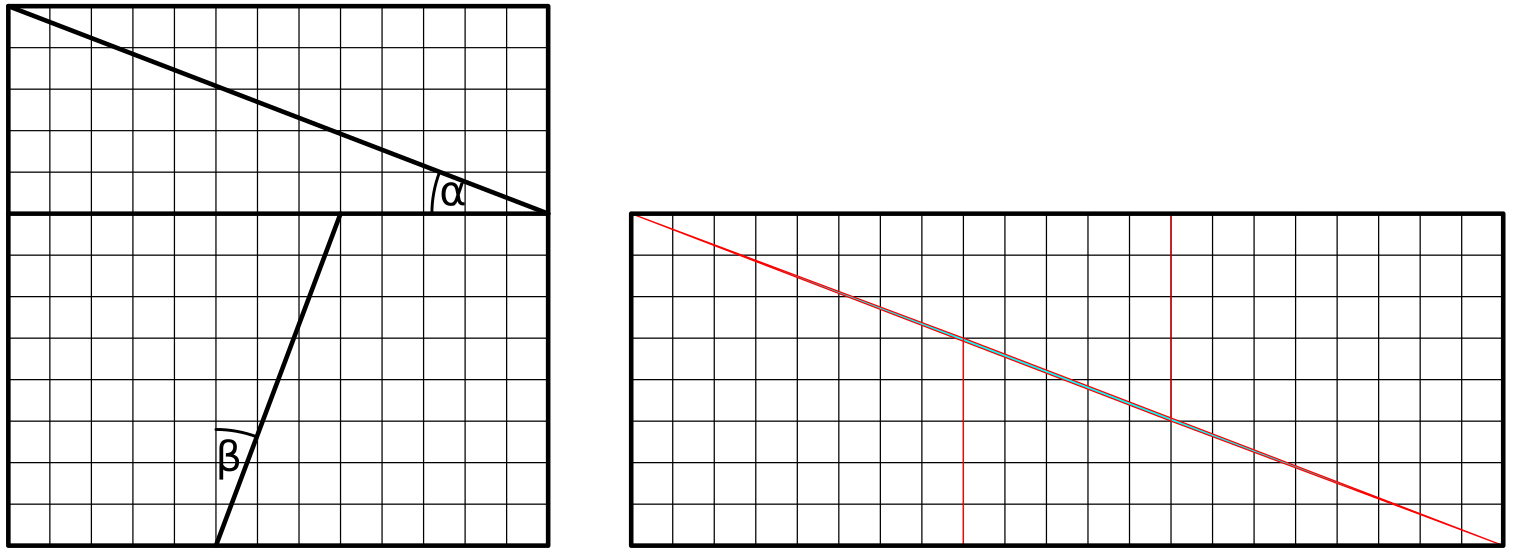
V jedné z předchozích úloh jsme předvedli čtverec 8x8, který byl po rozřezání na čtyři na dva lichoběžníky a dva trojúhelníky složen do tvaru obdélníku 13x5, který má o jeden čtvereček větší obsah než původní čtverec. Nyní máme obrácenou situaci. Na obrázku vlevo je čtverec 13x13, který má obsah 139 čtverečků. Po rozřezání podle vyznačených čar jsou dva trojúhelníky a dva lichoběžníky na obrázku vpravo složeny do tvaru obdélníku 21x8 o obsahu 168 čtverečků. Tentokrát se nám jeden čtvereček ztratil.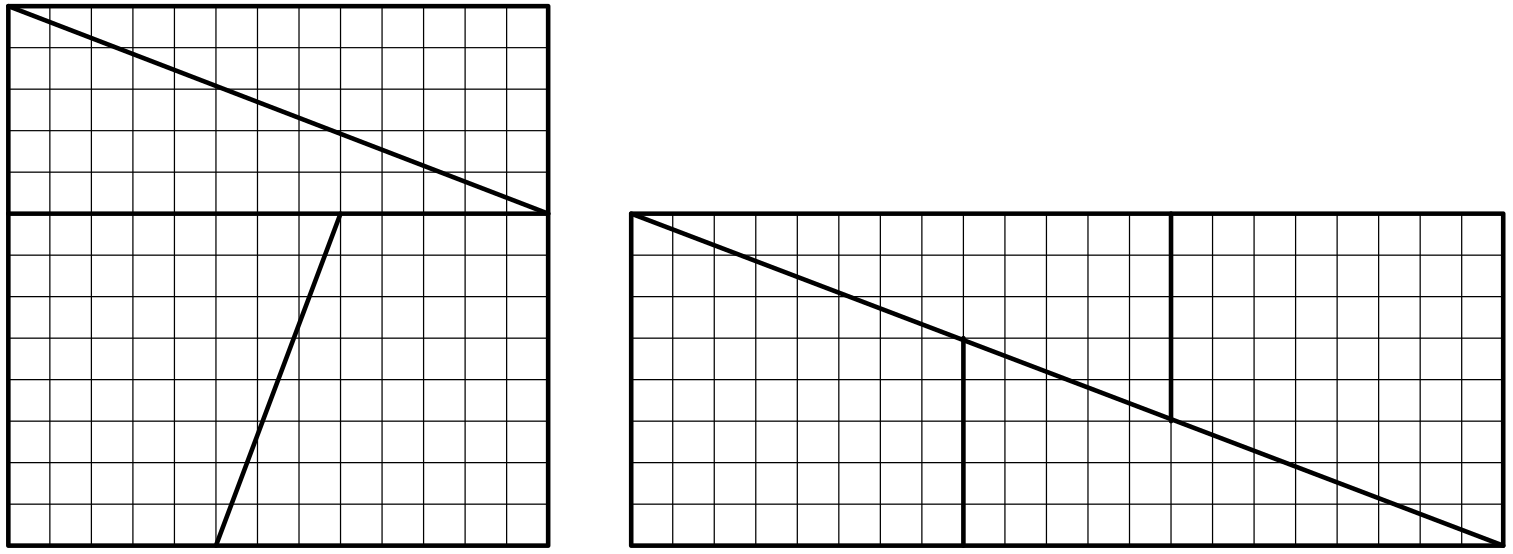

Jistě přijdete na to, kde je. Dokážete sestavit další úlohy tohoto typu?

Řešení

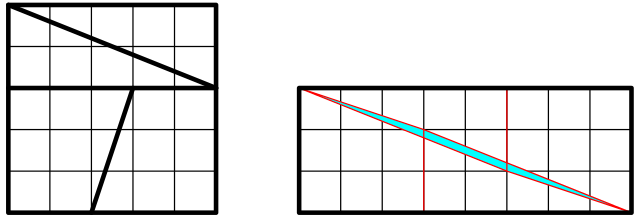
Paradox je opět jen zdánlivý. Silné čáry v zadání úlohy poněkud zakrývají skutečnost, že trojúhelníky a lichoběžníky sestavené do obdélníku k sobě nepřiléhají, ale tentokrát se trochu překrývají. Při vykreslení tenčími čarami je překryv o obsahu jednoho čtvereečku vidět. Z poměru stran je také vidět, že řezy oddělující trojúhelníky mají jiný sklon než řezy oddělující lichoběžníky: $\text{tg}\,\alpha={5\over13}\ne{3\over8}=\text{tg}\,\beta$.

Obdobných "paradoxních" úloh můžeme vytvořit libovolné množství. Všimněme si délek stran původního čtverce a výsledného obdélníku v minulé a v této úloze: $8$, $5$, $13$, $21$. Platí $5+8=13$, $8+13=21$. To jsou po sobě jdoucí členy posloupnosti tzv. Fibonacciho čísel $a_0=1$, $a_1=1$, $a_2=2$, $a_3=3$, $a_4=5$, $a_5=8$, $a_6=13$, $a_7=21$, $a_8=34$, ..., která je vytvořena tak, že první dva členy jsou jedničky a každý další člen je součtem předchozích dvou: $a_n=a_{n-1}+a_{n-2}$. Tato posloupnost pojmenovaná podle jednoho z nejvýznamnějších středověkých evropských matematiků Leonarda Pisánského zvaného Fibonacci má řadu pozoruhodných vlastností. Jednou z nich je identita $a_{n-1}a_{n+1}-a_n^2=(-1)^n$, která platí pro všechna přirozená čísla $n\ge1$ (důkaz se provede matematickou indukcí). Stačí tedy vzít čtverec o straně délky $a_n$, rozříznout ho na dva obdélníky o stranách $a_n$, $a_{n-1}$ a $a_n$, $a_{n-2}$, a tyto obdélníky dále rozříznout na dva trojúhelníky s odvěsnami $a_n$, $a_{n-2}$ a na dva lichoběžníky se základnami $a_{n-1}$, $a_{n-2}$. Na dalším obrázku je případ, kdy strana čtverce má délku $5:$

Je patrné, že "paradox" je tím méně viditelný, čím větší stranu čtverce použijeme.