Matematika pro poučení i pro zábavu

Úlohy pro zábavu i pro poučení

Hippokratovy měsíčky

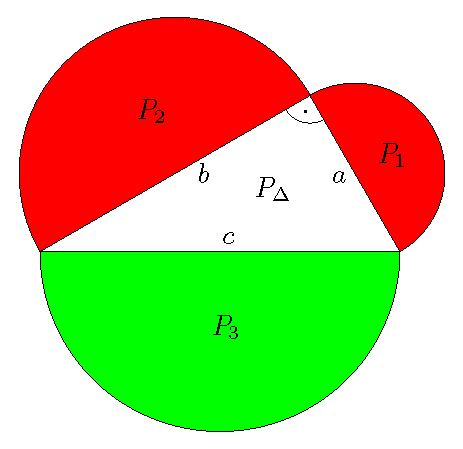
Snad každý zná jméno velkého řeckého matematika Eukleida (asi 325 př. n. l. – asi 260 př. n. l.), autora slavných Základů, nejúspěšnější knihy o matematice v historii. Méně je znám jeho předchůdce z 5. stol. př. n. l., Hippokratés z Chiu, který rovněž shrnul soudobé geometrické poznatky v knize nazvan0 Základy. Ta se téměř celá ztratila, informace o Hippokratově geometrii čerpáme především od jeho následovníků. Hippokratés je autorem pěkné úlohy, které se říká Hippokratovy měsíčky: Do půlkruhu vepišme pravoúhlý trojúhelník, jehož přeponou $c$ je průměr půlkruhu. (Podle Thaletovy věty leží třetí vrchol u pravého úhlu na oblouku půlkruhu.) Nad každou z odvěsen $a$, $b$ sestrojme půlkruh vně trojúhelníku. Tři půlkružnice vymezí dva Hippokratovy měsíčky. Určete velikost jejich celkové plochy. Hippokratés to dokázal před 2500 lety!

Řešení

Řešení lze nalézt snadno šikovným trikem bez složitého počítání. Převrátíme půlkruh nad přeponou, takže všechny tři půlkruhy budou vně trojúhelníku. Obrázek trochu připomíná Pythagorovu větu, že? Skutečně, podle Pythagorovy věty platí $c^2=a^2+b^2$. Vynásobíme-li obě strany rovnice číslem $\pi\over8$, dostaneme ${\pi\over8} c^2= {\pi\over8} a^2 +{\pi\over8} b^2$. Každý z těch tří výrazů vyjadřuje obsah půlkruhu nad přeponou, resp. nad příslušnou odvěsnou. Nyní překlopme půlkruh nad přeponou zpět. Vidíme, že obsah $P$ Hippokratových měsíčků dostaneme tak, že k obsahu trojúhelníku přičteme obsahy půlkruhů nad oběma odvěsnami a odečteme obsah půlkruhu nad přeponou, tj. $P=P_\Delta + P_1 + P_2 - P_3 = {1\over2} ab + {\pi\over8} a^2+ {\pi\over8}b^2 - {\pi\over8}c^2$. Protože ${\pi\over8} a^2 + {\pi\over8} b^2 - {\pi\over8} c^2=0$, zjistíme, že $P={1\over2} ab=P_\Delta$. Obsah obou Hippokratových měsíčků se rovná obsahu pravoúhlého trojúhelníku, nad kterým byly vytvořeny.